Can #n = 2#, #l = 2# describe an orbital?
1 Answer
No, it cannot.
Explanation:
As you know, we use four quantum numbers to describe the position and spin of an electron inside an atom.
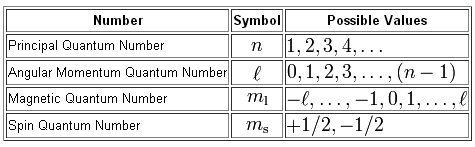
The three quantum numbers given to you describe the location of the electron inside an atom.
Now, the thing to notice here is that the value of the angular momentum quantum number,
#l = {0, 1, 2, ..., n-1}#
This means that
In your case,
#n = 2 implies l = {0, 1}#
Since

