What is the difference between an ideal gas and a real gas?
1 Answer
In summary, the realness of the gas is significant at high pressure and low temperature because its ground-state energy is more evenly distributed between linear, rotational, vibrational, and electronic energy levels, and because it takes up a molar volume unique to its identity.
An ideal gas is said to not "see" the other gases in the system:
- It collides elastically with the walls of the container (conserving kinetic energy).
- It does not interact with the other gases in the system.
- It takes up the same volume per mole at the same pressure and temperature as all other ideal gases.
Real gases differ in that:
- They collide inelastically with the walls of the container (using up some kinetic energy over time).
- They do interact with other gases in the system via attractive and/or repulsive forces.
- They take up a different volume per mole, even at the same pressure and temperature.
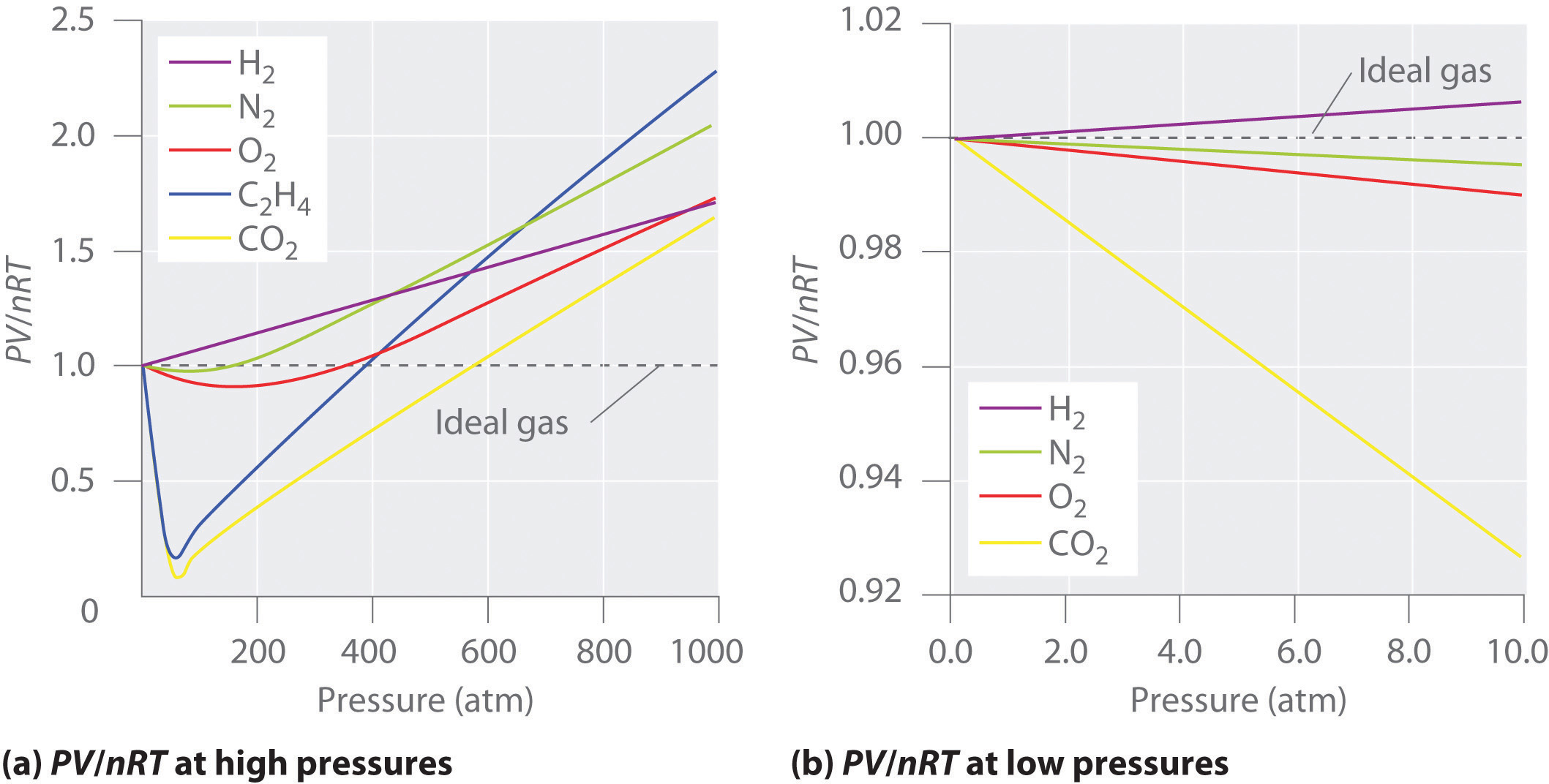
A real gas becomes more and more ideal at high temperature and low pressure because low pressure minimizes gas interactions (which also uniformizes the volume per mole), and high temperature minimizes inelasticity of collisions.
Deviation from ideal gas behavior is easily demonstrated in the difference in molar volume calculated in the ideal gas law and any of the real gas laws (such as van der Waals, Redlich-Kwong, Peng-Robinson, etc).
That should be obvious, because, say,
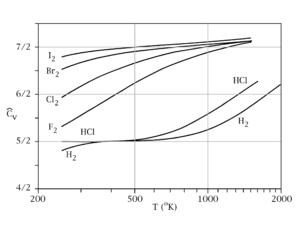
You could also look at this image and find that the (constant-volume) molar heat capacity approaches ideality at high temperatures, as we stated for the effect of temperature.
That is seen in the convergence onto a more similar
That's because the linear motion of the gas becomes more significant (average kinetic energy is directly proportional with the temperature) and overcomes the other contributions to the heat capacity of each real gas (rotational, vibrational, and electronic, i.e.

