Question #83abc
1 Answer
Oct 19, 2016
No useful factorization for
Explanation:
If
So, if
In our case
We know that
which has a null root.
Attached the null trace of
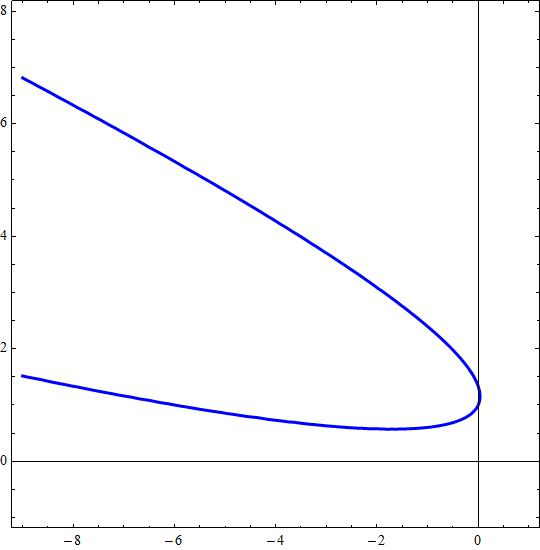
No useful factorization for
If
So, if
In our case
We know that
which has a null root.
Attached the null trace of
