Question

Question #fc13e

Answer 1

Let `y = arccot x`

Then `x = cot y`.

Differentiate implicitly to get

`1 = -csc^2 y * dy/dx`

So that `dy/dx = -1/csc^2 y`

Recall from trigonometry that `1+cot^2y = csc^2 y` so

`dy/dx = -1/(1+cot^2y)`

Finally replace `cscy` with `x` (from the second line of the explanation.)

`dy/dx = -1/(1+x^2)`

Answer 2

Use implicit differentiation.

Explanation:

We'll use implicit differentiation:

Let `y = "arccot"(x)`

`=> cot(y) = x`

`=> d/dxcot(y) = d/dxx`

`=> -csc^2(y)dy/dx = 1`

`=> dy/dx = -1/csc^2(y)`

Now let's see what `csc^2(y)` is in terms of `x`. Draw a right triangle with an angle `y` such that `cot(y) = x` (i.e. `y= "arccot"(x)`):

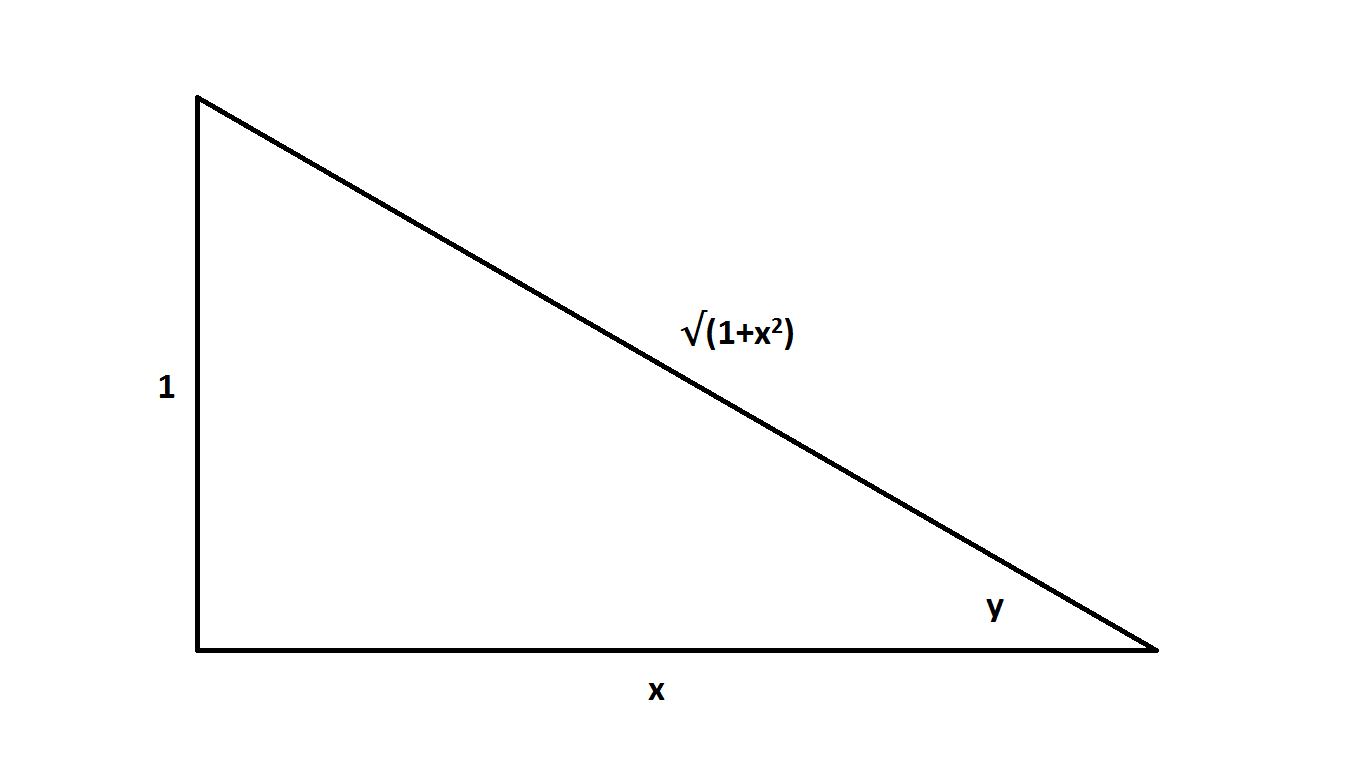
Setting the legs so that `cot(y) = x`, we can find the length of the hypotenuse as `sqrt(1+x^2)` using the Pythagorean theorem. Now we can calculate `csc^2(y)`.

`csc^2(y) = (csc(y))^2 = (sqrt(1+x^2)/1)^2 = 1+x^2`

Substituting this in, we arrive at our answer:

`("arccot"(x))' = dy/dx = -1/(1+x^2)`