Question #ee74d

1 Answer
A08
Jan 13, 2017

An object is released vertically downwards from a known height #h, "units (feet)"# with initial velocity #u=0, "units (feet per second)"# at time #t=0, "units second)"# and allowed to fall freely under the force of gravity as shown in the figure below.

As it reaches ground (#h=0#), the time is noted. Let it be #t#.

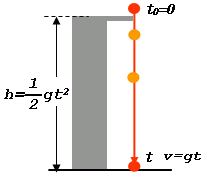
keisan.casio.jp

General Kinematic equation equation governing the free fall under gravity is
#h=ut+1/2g t^2#
Inserting given values and solving for #g# acceleration due to gravity we get
#h=0xxt+1/2g t^2#
#=>g=(2h)/t^2#, #"feet per second"^2#

Related questions
See all questions in Acceleration
Impact of this question
1467 views around the world
You can reuse this answer
Creative Commons License