Question

Question #34319

Answer 1

`DeltaH > 0`, `DeltaS > 0`

Explanation:

As you know, the only criterion that determines the spontaneity of a reaction is the Gibbs free energy change, `DeltaG`, which is defined as

`color(blue)(bar(ul(|color(black)(DeltaG = DeltaH - T * DeltaS)color(white)(a/a)|)))`

Here

`DeltaH` - the enthalpy change of reaction
`T` - the absolute temperature at which the reaction takes place
`DeltaS` - the entropy change of reaction

Now, in order for a reaction to be spontaneous at a given temperature, it must have

`DeltaG < 0`

This, of course, implies that a non-spontaneous reaction will have

`DeltaG > 0`

A positive Gibbs free energy change corresponds to

`DeltaH - T * DeltaS > 0`

This means that at low temperatures, you have

`DeltaH > T * DeltaS`

Now, this can be true for `DeltaH < 0` and `DeltaS < 0`. However, you are told that at high temperatures the reaction becomes spontaneous.

This means that you need

`DeltaH - T * DeltaS < 0`

or

`DeltaH < T * DeltaS`

As you can see, this cannot be true if `DeltaH < 0` and `DeltaS < 0` because increasing the value of `T` would simply make

`overbrace(DeltaH)^(color(blue)("negative")) > overbrace(T * DeltaS)^(color(blue)("even more negative")) ->` non-spontaneous reaction

However, if `DeltaH >0` and `DeltaS > 0`, increasing the value of `T` would make

`overbrace(DeltaH)^(color(darkgreen)("positive")) < overbrace(T * DeltaS)^(color(darkgreen)("even more positive")) ->` spontaneous reaction

Remember, `T` is always positive because it expresses absolute temperature.

In general terms, you can have four possible scenarios when dealing with the Gibbs free energy change

• `DeltaH<0`, `DeltaS>0 ->` spontaneous at any temperature
• `DeltaH>0`, `DeltaS<0 ->` non-spontaneous regardless of temperature
• `DeltaH>0`, `DeltaS>0 ->` spontaneous at a certain temperature range
• `DeltaH<0`, `DeltaS<0 ->` spontaneous at a certain temperature range

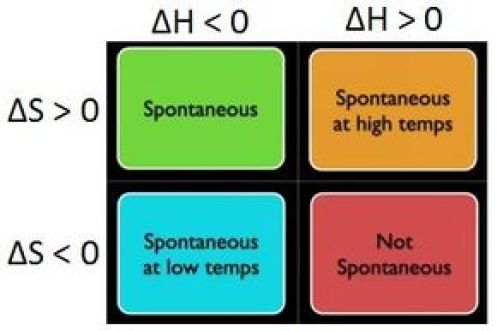
As you can see, reactions that have `DeltaH > 0` and `DeltaS > 0` are only spontaneous at high temperatures.

In this particular case, the reaction is endothermic, since `DeltaH > 0`, but the entropy change of the system overcomes the energy requirement at high temperatures.

A classic example would be the melting of ice, for which

• `DeltaH > 0 ->` you need to add heat to melt ice
• `DeltaS > 0 ->` the entropy of the system is increasing because you're going from solid to liquid

However, the melting of ice is only spontaneous when `T > "273.15 K"`, i.e. at temperatures above `0^@"C"`. When the temperature falls below `0^@"C"`, the melting of ice is a non-spontaneous process.