Show that # int_0^h int_0^x sqrt(x^2+y^2) dy dx = h^3/6 (sqrt(2) + ln( sqrt(2) + 1) ) #?
1 Answer
Explanation:
We want to evaluate:
so here
in the y-direction between
#y=0# and#y=x#
in the x-direction between#x=0# and#x=h# (a constant)
This represents a right angled triangle in the first quarter.
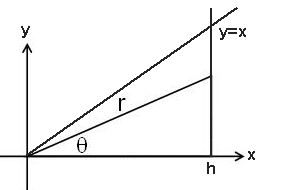
If we convert to Polar Coordinates then the region
an angle from
#theta=0# to#theta=pi/4#
a ray from#r=0# to#r=hsec theta# (as#cos theta = "adj"/"hyp"=h/r# )
And as we convert to Polar coordinates we get:
#x=rcos theta#
#y=rsin theta#
#dA = dy dy = r dr d theta#
So then the integrand
Hence,
NOTE
As this is an exercise in performing the double integral, I have used (without proof) the results:
#int sec^3x dx = 1/2secx tanx + 1/2ln|secx + tanx|#
And for clarity
# sec(pi/4)=sqrt(2), tan(pi/4)=1, sec 0=1, tan 0 =0 #

