Question

Question #e9bc7

Answer 1

`""_2^4"He" + ""_2^4"He" -> ""_4^8"Be"`

Explanation:

The thing to remember about nuclear equations is that they must conserve mass and charge.

In other words, the overall mass number and the overall atomic number must be equal on both sides of the equation.

In your case, you're dealing with a fusion reaction in which two helium-4 nuclides, `""^4"He"`, also called alpha particles, fuse to form a new element, beryllium, `"Be"`. Start by grabbing a periodic table and looking for the atomic number of the two elements, i.e. of helium and of beryllium.

You will find

`"For He: " Z = 2`

`"For Be: " Z = 4`

Now, in isotope notation, the atomic number is added to the bottom-left and the mass number is added to the top-left of the chemical symbol.

You will thus have

`""_2^4"He" ->` isotope notation for helium-4

`""_4^A"Be" ->` isotope notation for the resulting isotope

Your goal now is to find the value of `A`, the mass number of the beryllium isotope. You can now write

`""_color(blue)(2)^color(orange)(4)"He" + ""_color(blue)(2)^color(orange)(4)"He" -> ""_color(blue)(4)^color(orange)(A)"Be"`

Notice that you have

`color(blue)(2) + color(blue)(2) = color(blue)(4) ->` charge is conserved

You also need to have

`color(orange)(4) + color(orange)(4) = color(orange)(A) ->` mass must be conserved as well

The value of `A` will thus be

`4 + 4 = A implies A = 8`

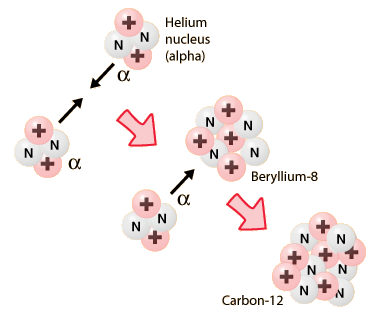
Therefore, the resulting isotope is beryllium-8 and the balanced nuclear equation that describes this fusion reaction looks like this

`""_2^4"He" + ""_2^4"He" -> ""_4^8"Be"`

As a side note, notice what happens when the beryllium-8 isotope fuses with another alpha particle

`""_ 4^8"Be" + ""_ 2^4"He" -> ""_ (color(white)(1)6)^12"C"`

The resulting nuclide is carbon-12, the most abundant isotope of carbon.