What symmetry operations leave trans-1,3-dichlorocyclobutane invariant?
1 Answer
You can carry out four symmetry operations on trans-1,3-dichlorocyclobutane.
Explanation:
The structure of trans-1,3-dichlorocyclobutane is
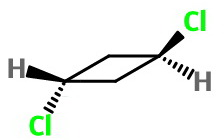 Structure
Structure
The ring is puckered, but it undergoes a rapid ring flip between the two bent forms.
We can treat the ring as if it were planar. However, at low temperatures the two conformations would be "frozen out" and the ring would have a different symmetry.
The planar molecule has
This point group contains four symmetry operations:
bbhat"E" color(white)(ml)"the identity ('do nothing') operation"ˆEmlthe identity ('do nothing') operation
bbhat"C"_2 color(white)(m)"a rotation about a two-fold axis"ˆC2ma rotation about a two-fold axis
bbhat"i" color(white)(mm)"inversion about a single point"
bbhatsigma_h color(white)(m)"reflection about the mirror"
" "" ""plane perpendicular to the C"_n
" "" "color(white)(l)"axis of the highest n"
Let's apply these operations to the molecule.
This one is easy. It amounts to doing nothing to the molecule.
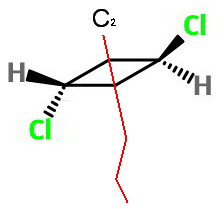 Rotation
Rotation
The
Rotation by 180° about this axis interchanges the two
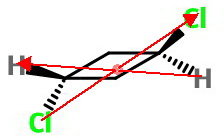 Inversion
Inversion
There is a centre of inversion at the mid-point of the ring.
Inversion through this point interchanges the two
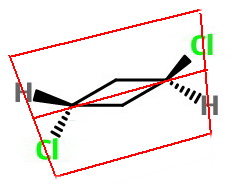 Reflection
Reflection
A mirror plane passes through the
It divides the molecule into two front and back mirror-image halves, and bisects the ring, while being coplanar with the explicit
The operation reflects carbons 2 and 4, but the remainder of the atoms stay in place.


