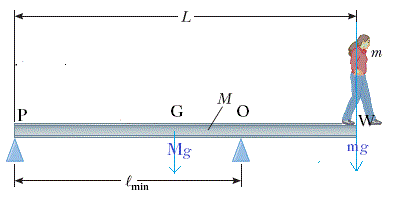
To find out the minimum value of #l" ie "l_"min"# so that the woman can walk towards the other end W of the beam without tipping,we can say, when the woman reaches at the other end the moment of the weight of the beam (Mg) at G, the mid point of the beam and the moment of the weight of the woman (mg) at W about 2nd pivot at O are equal for #l=l_"min"#
Hence we can write
#OWxxmg=OGxxMg#
#=>(PW-PO)xxmg=(PO-PG)xxMg#
#=>(L-l_"min")mg=(l_min-L/2)Mg#
#=>(L-l_"min")/(l_"min"-L/2)=M/m#
#=>(L-l_"min")/(l_"min"-L/2)+1=M/m+1#
#=>(L/2)/(l_"min"-L/2)=(M+m)/m#
#=>(L/2)=(l_"min"-L/2)xx(M+m)/m#
#=>(l_"min"-L/2)=L/2xxm/(M+m)#
#=>l_"min"=L/2xxm/(M+m)+L/2#
#=>l_"min"=L/2(m/(M+m)+1)#
#=>l_"min"=((2m+M)/(2M+2m))*L#



