Question

Question #05570

Answer 1

`x = 1/3(8-sqrt(19)) = 1.214` Corresponds to the maximum volume.

`:. x = 1.2` inches

The associated max volume is given by:

`\ \ \ \ \ V = 4x^3-32x^2+60x`
`:. V=32.8` cubic inches

Explanation:

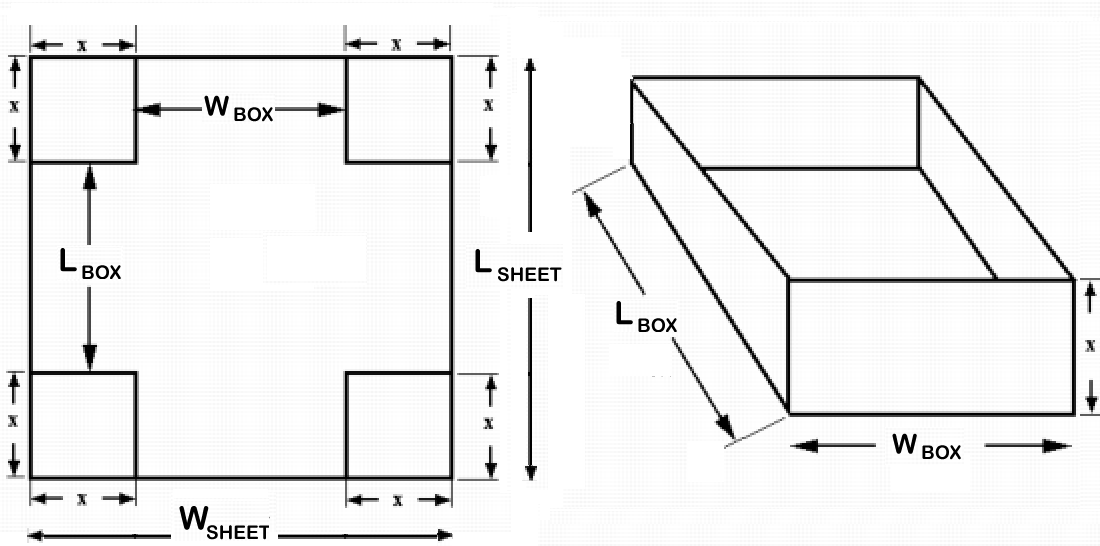
Let us set up the following variables:

`{(w, "Width of the Box (in)"), (l, "Length of the Box (in)"), (x, "Length of the Corner Cut-out (in)"), (V, "Volume of the Box (cubic in)") :}`

We want to vary the corner length `x` such that we maximise `V`, ie find a critical point of `(dV)/dx` that is a maximum, so we to find a function `V=V(x)`.

The dimensions of the sheet are 6" by 10", hence, wlog taking `w=6` we get:

Width: `x+w+x=6 \ \ => w=6-2x = 2(3-x)`
Length: `x+l+x=10 => l=10-2x = 2(5-x)`

Then the volume is given by:

`\ \ \ \ \ V=wlx`
`:. V = 2(3-x)2(5-x)x`
`:. V = 4x(x^2-8x+15)`
`:. V = 4x^3-32x^2+60x`

Differentiating wrt `x` gives us;

`:. (dV)/dx=12x^2-64x+60`

At a critical point, `(dV)/dx=0`

`:. 12x^2-64x+60 = 0`
`:. 3x^2-16x+15 = 0`

To solve this quadratic I will complete the square:

`x^2-16/3x+5 = 0`
`:. (x-16/6)^2-(16/6)^2+5 = 0`
`:. (x-16/6)^2= 256/36-5`
`:. (x-16/6)^2= 19/9`
`:. x-16/6= +-sqrt(19)/3`
`:. x= 16/6+-sqrt(19)/3`
`:. x = 1/3(8+-sqrt(19))`
`:. x=1.214, 4.120` (3dp)

We should check while value leads to a maximum volume

`:. (d^2V)/dx^2=24x-64`

`x = 1/3(8-sqrt(19)) => (d^2V)/dx^2 < 0 => max`
`x = 1/3(8+sqrt(19)) => (d^2V)/dx^2 > 0 => min`

graph{4x^3-32x^2+60x [-5, 5, -30, 40]}

Hopefully you can visually confirm the above #