Question

Question #75d40

Answer 1

Focus of the parabola is `(6, -1)`

`x^2=16y`

Explanation:

Given -

`12(x-3)=(y+1)^2`

It can be written as -

`(y+1)^2=12(x-3)`

Since it is in the form `y^2=4ax`; it opens to the right

This is in the form-

`(y-k)^2=4a(x-h)`

Where -

`(h,k)` is vertex
`a` is distance of focus or directrix from the vertex.

From the given equation we can find the value of `a`. For this, we have to rewrite the equation like this.

`(y+1)^2=4xx3(x-3)^3`

Then `a=3`
Vertex `(3,-1)`

focus `(6, -1)`

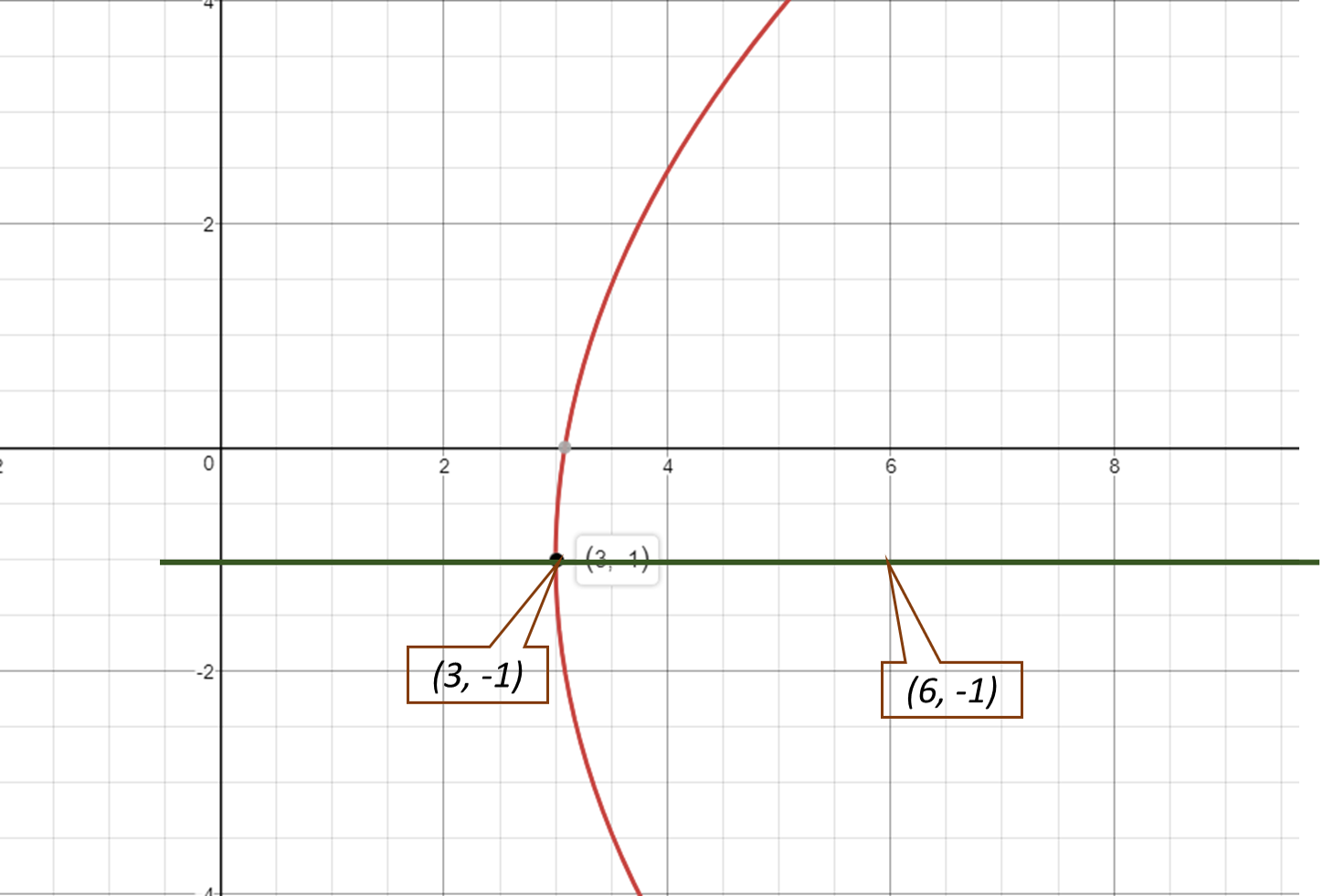
PROBLEM 2

Given -

Focus `(0, 4)`
Directrix `y=-4`

Look at the graph

Vertex is a point of the parabola.

Vertex lies at equi distance in between focus and directrix.

The coordinates of the point at which the directrix cuts the axis of symmetry is `(0, -4)`

Then the coordinates of the vertex `(0+0)/2, (4-4)/2= (0, 0)`

Vertex `(0, 0)`. It is a point on the parabola.

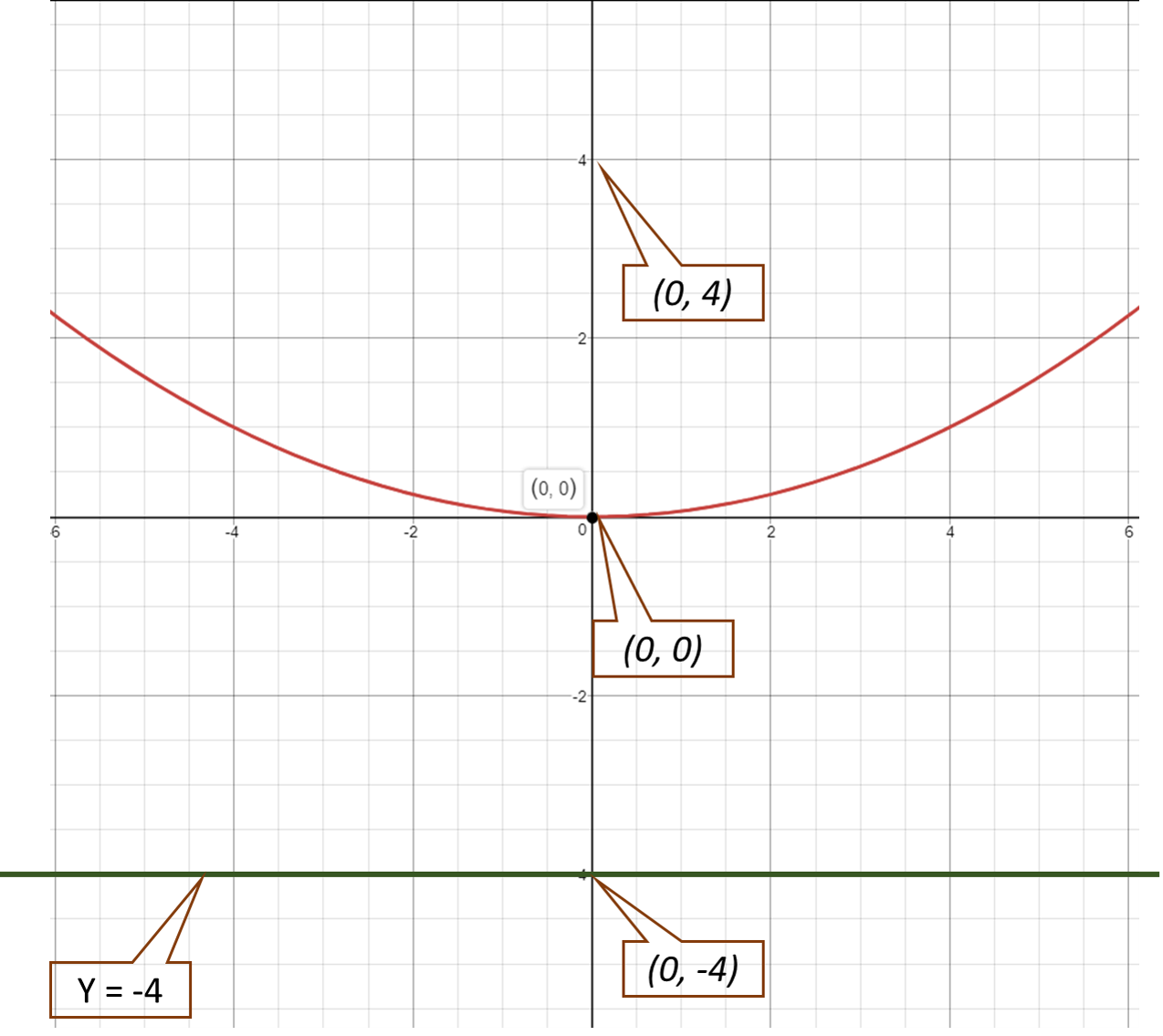
As we know the vertex, we can form the equation.

The equation of the parabola which opens up and whose vertex is at origin is `x^2=4ay`

We know `a` is the distance between focus and vertex.

`a=4`

then, the equation is -

`x^2=16y`