Solve #{(x^y=y^x),(x^2=y^3):}# ?
1 Answer
Dec 10, 2016
Explanation:
Now applying
we obtain
Dividing term to term we obtain the relationship
The solutions for (1) are obtained solving
and
so they are
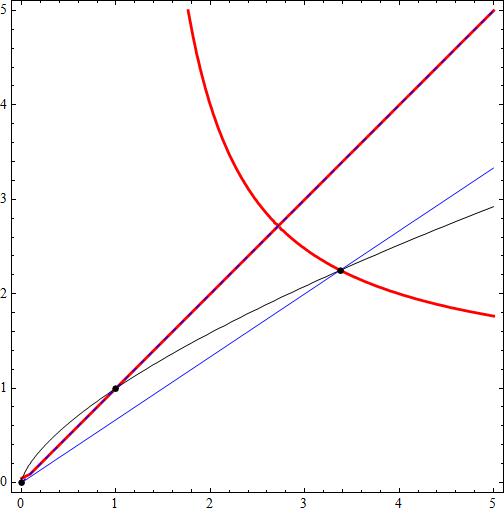
Attached a figure showing the interceptions
In red the two leafs of
blue dotted
blue continuous
black
The intersections have a black dot over.
The solution at