Consider a normal equation in #x# such as:
#3x=6#
To solve this equation you simply take the #3# in front of #x# and put it, dividing, below the #6# on the right side of the equal sign.
#x=6/3=3^-1*6=2#
at this point you can "read" the solution as: #x=2#.
With a system of #n# equations in #n# unknowns you do basically the same, the only difference is that you have more than 1 unknown (and equation) that can now be represented by matrices and by the inverse matrix in place of the coefficient to the -1 (in our example is #3^-1#).
You can use matrices and change your system in a matrix equation :
If you have the following system:
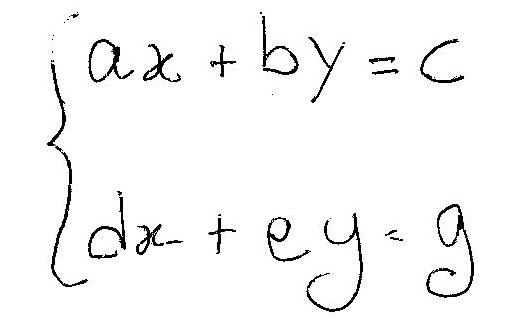
(where #a,b,c,d,e,g# are real numbers)
you can change it in a matrix equation:
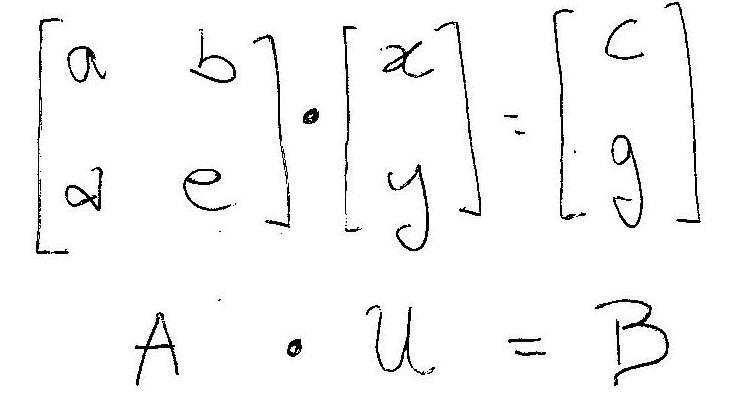
Where #A# is the matrix of the coefficients of the unknowns, #U# is the column of the unknown and #B# is the column of the pure coefficients (without unknowns).
You can check that this representation with matrices represents the system by doing the multiplication #A*U# and setting it equal to #B# you'll get back your original system!!!
Now, to solve your matrix equation #A*U=B# you can multiply both sides by the inverse of #A#, i.e. #A^-1#
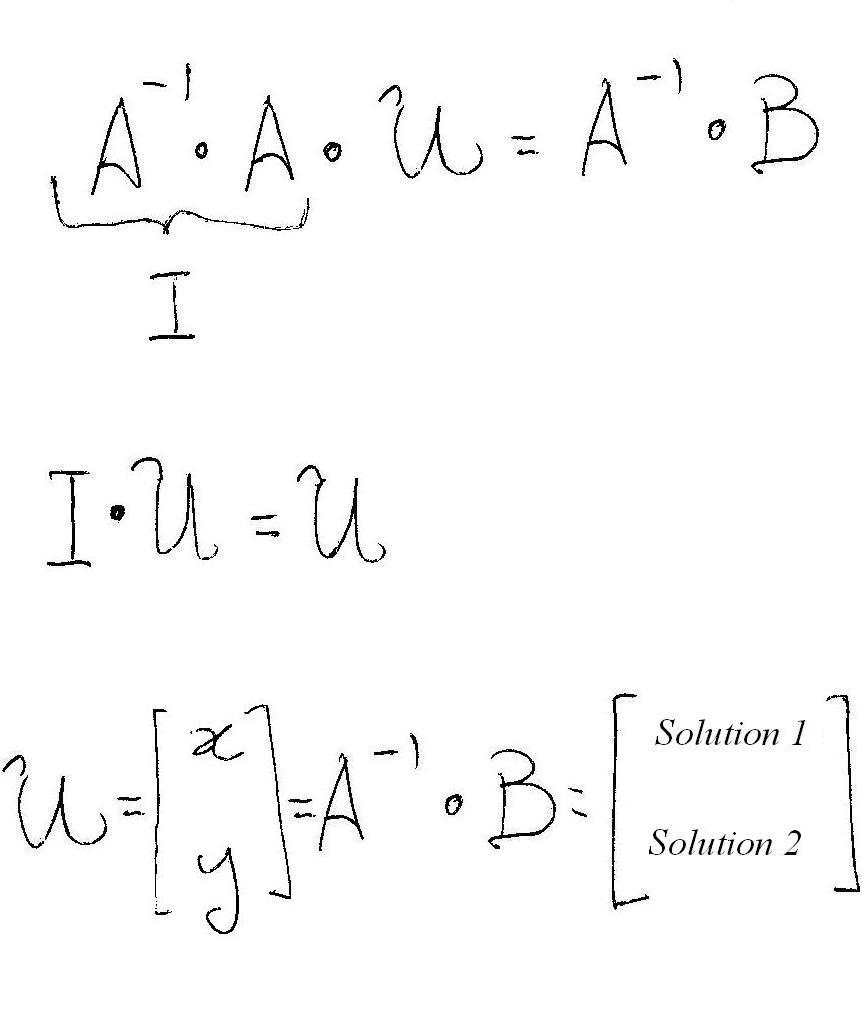
(Remembering that #I# is the identity matrix .
For example:
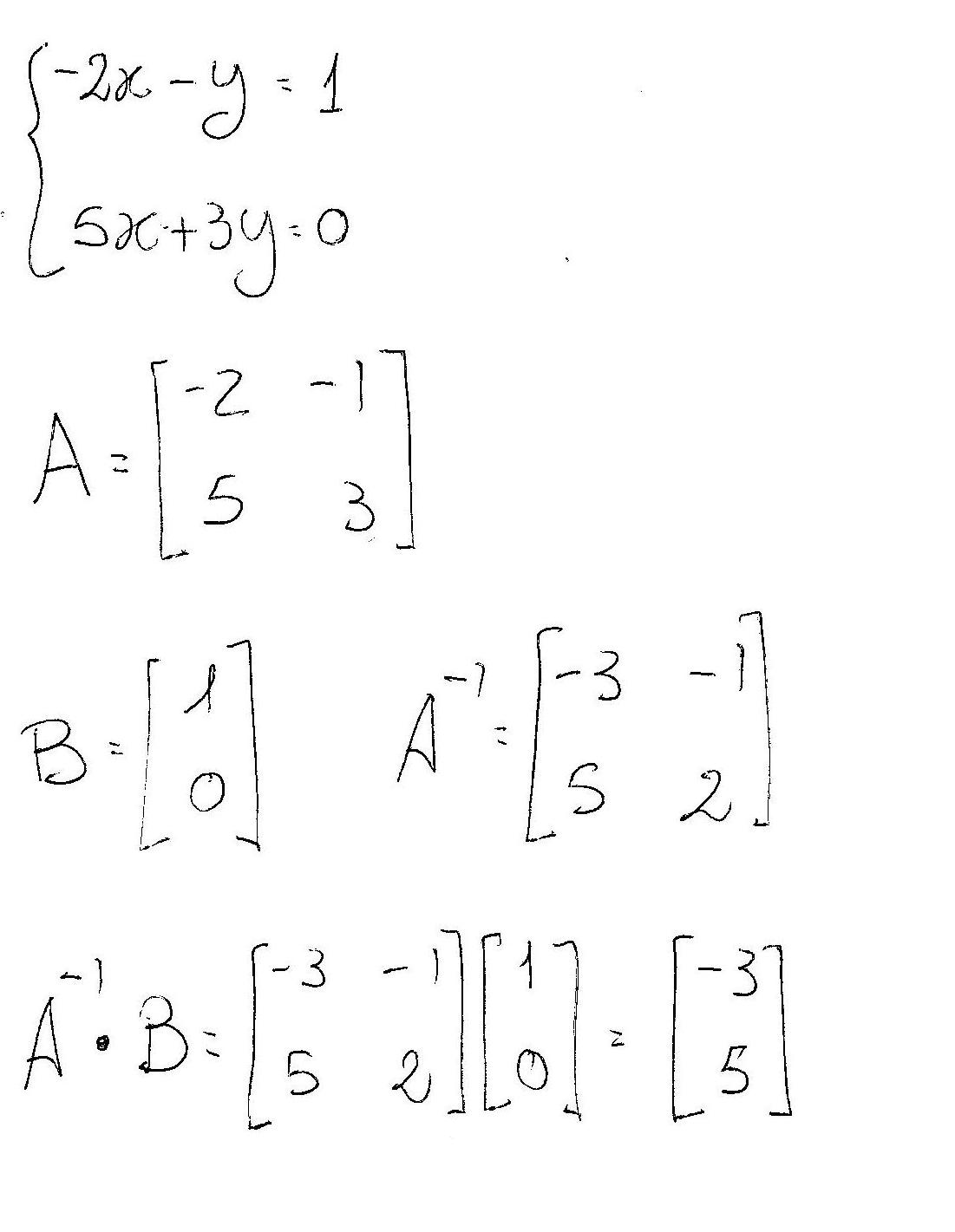
So:
#x=-3#
#y=5#

