Refer to the figure below
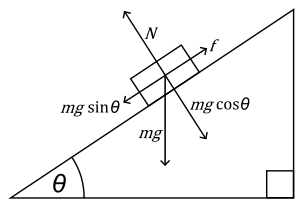
As the mass slides down the inclined plane, we see that Normal reaction #N# is equal and opposite to the #cos theta# component of the weight. The other two forces acting on the mass are, #sin theta# component acting along the plane and force of friction acting up the plane and opposing the motion of the mass. _"net"
As there is movement in sliding down there is net force given as
#F_"net"=mgsin theta-f#
Using Newton's second law this net force can be written as
#F_"net"=ma# .......(1)
Where #m# is mass #and a# is acceleration produced.
Using the kinematic equation
#s=ut+1/2at^2# and inserting given quantities in SI units we get
#1.2=0xx0.42+1/2a(0.42)^2#
Solving for #a#
#a=1.2xx2/(0.42)^2 =13.605ms^-2#, rounded to three decimal places
Inserting value of #a# in (1)
#F_"net"=4.5xx13.605#
#=>F_"net"=61.22N#

