Question

Question #a40d8

Answer 1

see explanation.

Explanation:

Let `angleEAD=x, angleADC=y`
Given `AE=EF, => angleEFA=x, => angleBFD=x`

Sine Law :

`DeltaACD, (CD)/sinx=(AC)/siny ----- (1)`
`DeltaBFD, (DB)/sinx=(BF)/sin(180-y)=(BF)/siny-----(2)`

Given `CD=DB, (CD)/sinx=(DB)/sinx, => (1)=(2)`
`=> (AC)/siny=(BF)/siny, (sin(180-y)=siny)`

Hence, `AC=BF` (proved)

Answer 2

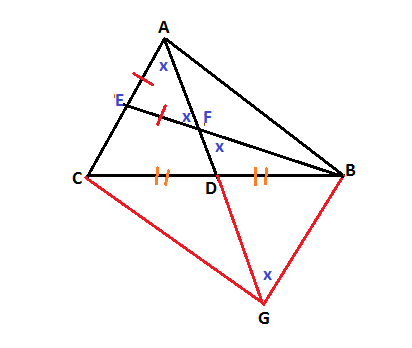
Given ABC a triangle where [AD] is the median and let the segment line [BE] which meets [AD] at F and [AC] at E If we assume that AE=EF, we are to show that AC=BF.

Construction

AD is extended up to G such that `AD=DG` and the point G is joined with C,D and B.

Proof

Now in quadrilateral `ABGC`, D the point of intersection of two diagonals is the mid point of the diagonals as `CD=DB ("given");AD =DG("by construction")` So quadrilateral `ABGC` is a parallelogram.

In `Delta AEF`
`AF=FE->/_FAE=/_AFE=/_BFG ("vertically opposite")`
`=>/_CAG=/_BFG`

Again `AC |\| BG` and AG intercept
So `/_CAG="alternating"/_AGB=/_BGF`

So `/_BFG=/_BGF->BF=BG`
Again `BG=AC("opposite sides of a parallelogram")`

Hence `AC=BF`