Question

Question #d4070

Answer 1

The answer is very simple: the difference is in the object on which the forces act. An action-reaction pair is not canceled. On the other hand, balanced forces do.

Explanation:

Consider the following image:

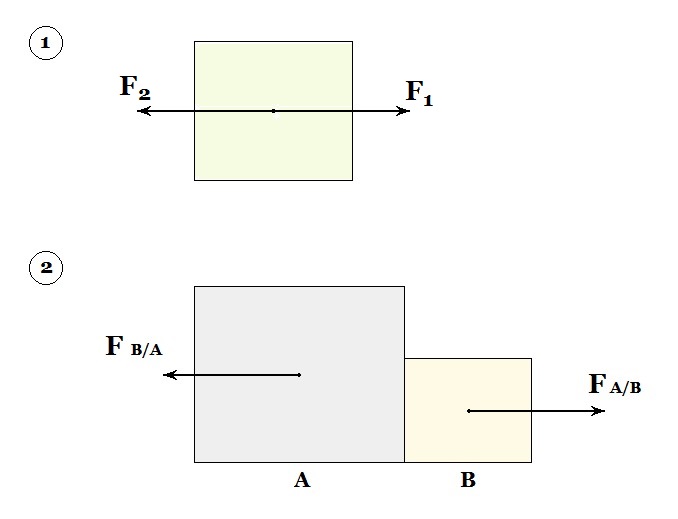
Consider case 1:

On a body two forces of the same modulus and direction act but opposite directions, `F_1` and `F_2`. Therefore, the resultant `F_R` of the forces acting on said body is 0, because:

`F_2 = F_1 rArr F_R = F_1 - F_2 = 0`

Instead, let's see what happens in case 2:

Here, we have a body `A` that exerts a force `F_{A//B}` on a body `B`. By virtue of Newton's Third Law, we can state that on the body `A` will appear a force `F_{B//A}` exerted by the body `B`.

That is, to the `F_{A//B}` action responds an `F_{B//A}` reaction.

But these forces, being of equal modulus and opposite senses, do not cancel out. Why? Because they act on different bodies . The resulting force on `A` is `F_R = F_{B//A}`, while on `B` there is a resulting force `F_R = F_{A//B}`. When acting on different bodies they are independent forces and each body will move according to the acceleration that each of these forces provoke on him, i.e.:

`a_A = - {F_{B//A}}/{m_A} color(white) ".................." a_B = {F_{A//B}}/{m_B}`

Where we have assumed that the left-right direction is the positive.