Question #03b61
1 Answer
Here's why that is the case.
Explanation:
As you know, we can use a total of four quantum numbers, which make up a quantum number set, to describe the location and spin of an electron in an atom.
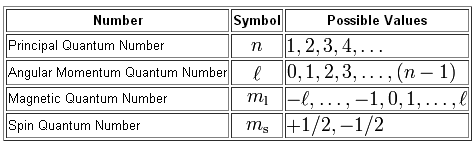
The notation used for a quantum number set is
#(n, l, m_l, m_s)#
The quantum number set given to you cannot describe an electron in an atom because the value of the angular momentum quantum number,
As you can see, the angular momentum quantum number can take values in the range
#l = {0, 1, 2, ..., n-1}#
where
In your case, you have
#(color(red)(n), color(blue)(l), m_l, m_s) = (color(red)(2), color(blue)(2), -1, -1/2)#
Since
#n=2 implies l= {0, 1}#
Since you have

