Question

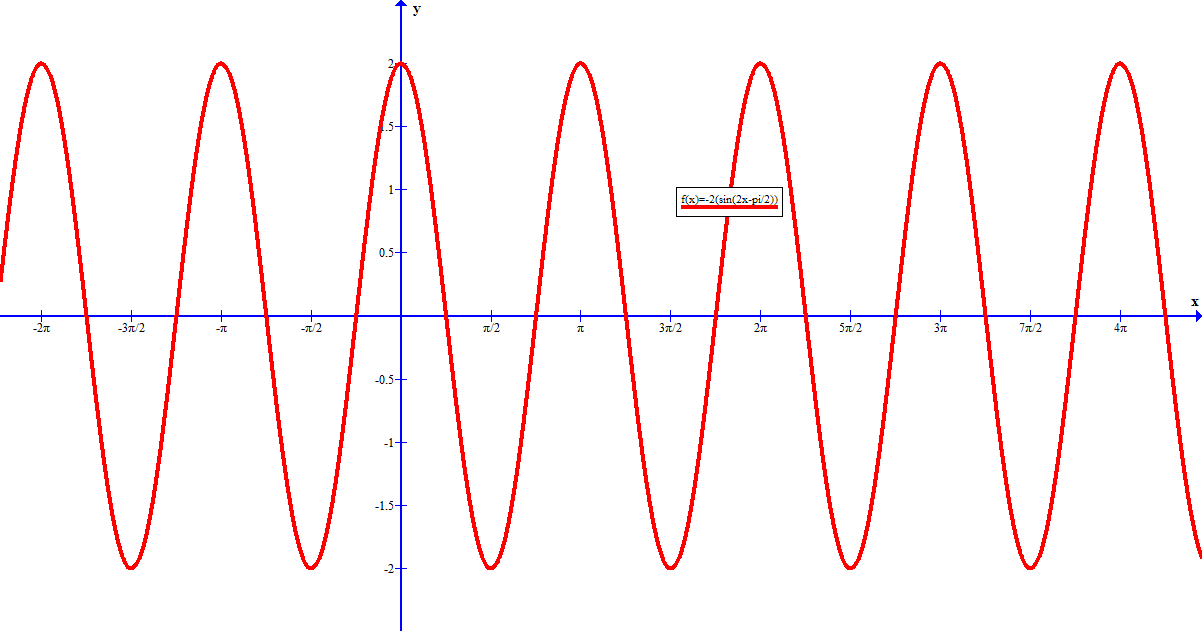
How do you graph `sin(2x-pi/2)`?

Answer 1

= 2cos (2x)

Explanation:

Use trig unit circle and property of complement arcs:
y = - 2sin (2x - pi/2) = 2cos (2x)

Answer 2

See below for step-by-step analysis and graphing

Explanation:

Let's start with the standard `color(black)(sin(x))` function
and in particular let's note the basic cycle of the `sin(x)` function:

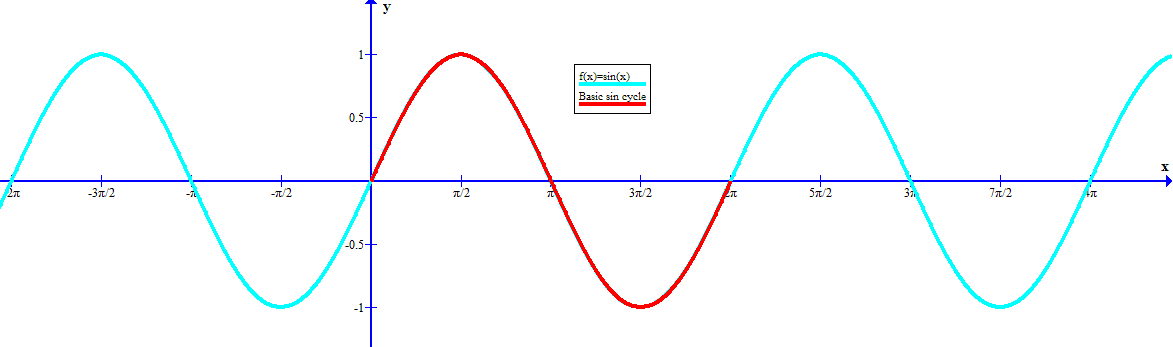
Notice that the argument range for the basic cycle is `[0,2pi]`

`color(magenta)("<><><><><><><><><><><><><><><><><><><><><><><><><><><> ")`

Now let's consider what happens with `sin(x-pi/2)`
The basic cycle still requires an argument range of `[0,2pi]`,
that is `(x-pi/2) in [0,2pi]`
but for this to be possible, `x in [pi/2,(5pi)/2]`

That is the basic cycle will appear to have shifted to the right by `pi/2`

`color(magenta)("<><><><><><><><><><><><><><><><><><><><><><><><><><><> ")`

Next let's consider what happens when we double the value of the variable `x` causing the argument expression to become `(2x-pi/2)`
The basic cycle still needs an argument range `[0,2pi]`,
that is `(2x-pi/2) in [0,2pi]`
which, as we have seen, implies `2x in [pi/2,(5pi)/2]`
which, to be possible, means `x in [pi/4,(5pi)/4]`

The horizontal distance from the origin on the X-axis seems to have been "squeezed" by a factor of `1/2`

`color(magenta)("<><><><><><><><><><><><><><><><><><><><><><><><><><><> ")`

Finally, what happens to our basic cycle when we multiply the entire expression by `(-2)` to get `y=-2sin(2x-pi/2)`?
The value of each y-coordinate is scaled by a factor of `2`
(you might think of this as the coordinate is reflected in the X-axis and then stretched by `2` away form the X-axis).

`color(magenta)("<><><><><><><><><><><><><><><><><><><><><><><><><><><> ")`

Of course, this only gives us the basic cycle.

For the full graph this cycle is repeated infinitely in both directions: