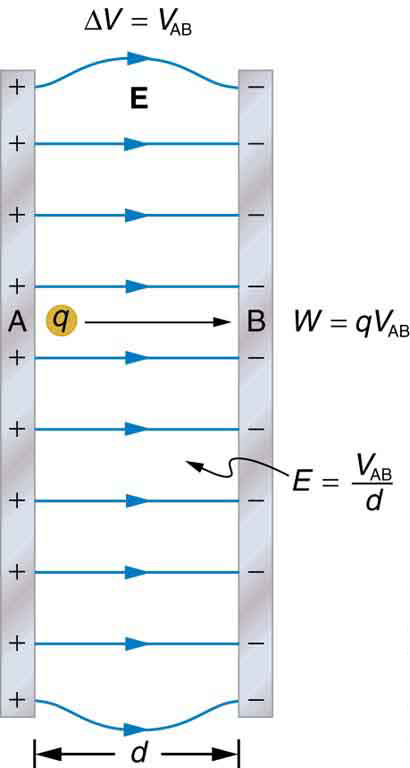
An electric field #vecE# will exist between any two points due to presence of potential difference between these points.
The product of any charge #q# and of the difference in electric potential between any two points #Aand B#, by definition, is the difference in electric potential energy of that charge between those points. Therefore,
# P_B- P_A = qxx(V_B - V_A) J#
Therefore, when a charged particle is released from rest in a uniform electric field, the corresponding electric potential at the particle's changing locations changes.
The total energy #E# of the electron consists of its electric potential energy #PE#, and the kinetic energy #KE#. Hence,
# E = PE + KE#
where we know that if #mand v# be mass and velocity respectively of the charged particle.
# KE = \frac{1}{2} \m\ v^2#
These are depicted in the figure below.
For electron.
Initially, #KE=0#, as it is at rest. It has #PE# due to potential difference or due to electric field. Also due to #-ve# charge of electron its #PE# is #-ve#. As electron is accelerated towards #+ve# potential, its #KE# increases and potential energy decreases. Clearly electric potential at the electron's changing locations must increase so that it accelerates forward.
For proton.
As in the case of electron, proton's initial #KE=0#. Proton also has #PE# due to potential difference or due to electric field. However, due to its #+ve# charge its #PE# is #+ve#. As positive charge accelerates towards #-ve# potential its #KE# increases and potential energy decreases. Since it is accelerating towards #-ve# potential, electric potential at the proton's changing locations must decrease so that it accelerates forward.
Hope it helps.

