How do you prove #sin^2x + cos^2x = 1#?
2 Answers
See explanation...
Explanation:
Consider a right angled triangle with an internal angle
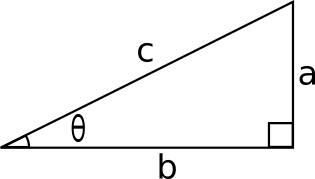
Then:
#sin theta = a/c#
#cos theta = b/c#
So:
#sin^2 theta + cos^2 theta = a^2/c^2+b^2/c^2 = (a^2+b^2)/c^2#
By Pythagoras
So given Pythagoras, that proves the identity for
For angles outside that range we can use:
#sin (theta + pi) = -sin (theta)#
#cos (theta + pi) = -cos (theta)#
#sin (- theta) = - sin(theta)#
#cos (- theta) = cos(theta)#
So for example:
#sin^2 (theta + pi) + cos^2 (theta + pi) = (-sin theta)^2 + (-cos theta)^2 = sin^2 theta + cos^2 theta = 1#
Pythagoras theorem
Given a right angled triangle with sides
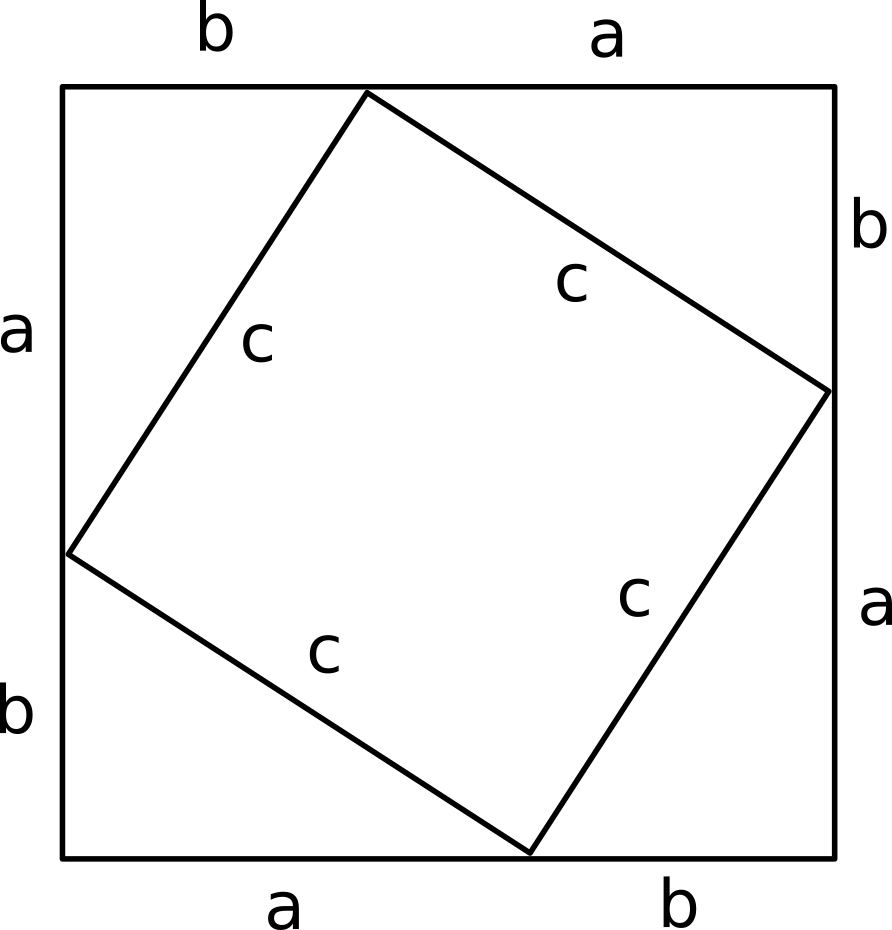
The area of the large square is
The area of the small, tilted square is
The area of each triangle is
So we have:
#(a+b)^2 = c^2 + 4 * 1/2ab#
That is:
#a^2+2ab+b^2 = c^2+2ab#
Subtract
#a^2+b^2 = c^2#
Use the formula for a circle
Explanation:
The formula for a circle centred at the origin is
#x^2+y^2=r^2#
That is, the distance from the origin to any point
Picture a circle of radius
graph{(x^2+y^2-1)((x-sqrt(3)/2)^2+(y-0.5)^2-0.003)=0 [-2.5, 2.5, -1.25, 1.25]}
If we draw a line from that point to the origin, its length is
graph{(x^2+y^2-1)(y-sqrt(3)x/3)((y-0.25)^4/0.18+(x-sqrt(3)/2)^4/0.000001-0.02)(y^4/0.00001+(x-sqrt(3)/4)^4/2.7-0.01)=0 [-2.5, 2.5, -1.25, 1.25]}
Let the angle at the origin be theta (
Now for the trigonometry.
For an angle
#sin theta = "opp"/"hyp" = y/r" "<=>" "y=rsintheta#
Similarly,
#cos theta = "adj"/"hyp"=x/r" "<=>" "x = rcostheta#
So we have
#" "x^2" "+" "y^2" "=r^2#
#(rcostheta)^2+(rsintheta) ^2 = r^2#
#r^2cos^2theta + r^2 sin^2 theta = r^2#
The
#cos^2 theta + sin^2 theta = 1#
This is often rewritten with the
#sin^2 theta + cos^2 theta = 1#
And that's it. That's really all there is to it. Just as the distance between the origin and any point


