Question

Question #a76f9

Answer 1

`x+4y+-3=0`. See the tangents-inclusive Socratic graph.

Explanation:

The equations have the form

`y=-1/4x+c`.

The tangent lines meet the hyperbola x y = 9 in two coincident

points.

Eliminating y and equating the discriminant of the quadratic

`x(-1/4x+c)=9` to 0,

`c^2-9=0`, giving `c = +-3`.

graph{(xy-9)((y+x/4)^2-9)=0 [-40, 40, -20, 20]}
.

Answer 2

The equations of the two tangents that have gradient `-1/4` are (without loss of generality):

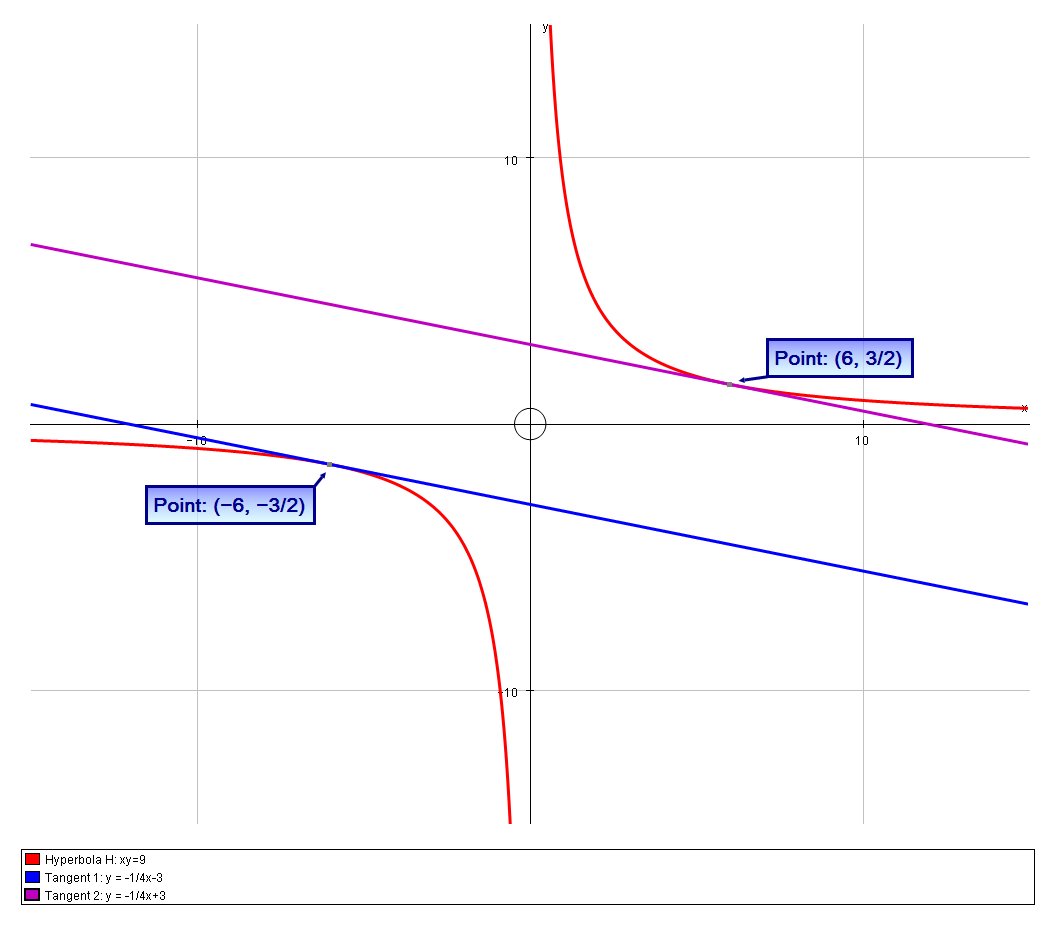
`l_1: \ \ \ y = -1/4x-3`
`l_2: \ \ \ y = -1/4x+3`

Explanation:

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point.

The equation of the given hyperbola, `H`, is:

`xy = 9`

Differentiate (implicitly and product rule) the equation of the hyperbola:

`(x)(dy/dx)+(1)(y) = 0`
`:. dy/dx = -y/x`

A generic point on the hyperbola can be parametrised with a parameter `t` as follows:

`x= t => yt=9 => y=9/t`

So a generic point has coordinates `P(t, 9/t)`. Thus, the gradient of the tangent at `P` is given by:

`dy/dx = -y/x = -(9/t)/(t) =-9/t^2`

At the point where the gradient of the tangent is `-1/4` we have:

`-9/t^2 = -1/4`
`:. t^2=36`
`:. t=+-6`

(NB We expected two solutions as there are two tangents!)

Case 1
When `t=-6 => P(t,1/t)=(-6,-3/2)`
So, the tangent passes through `(-6,-3/2)` and has gradient `-1/4`,
so using the point/slope form of a straight line `y-y_1=m(x-x_1)` the equation we seek is;

`y-(-3/2)=(-1/4)(x-(-6))`
`:. y+3/2 = -1/4x-3/2`
`:. y = -1/4x-3`

Case 2
When `t=6 => P(t,1/t)=(6,3/2)`
So, the tangent passes through `(6,3/2)` and has gradient `-1/4`,
so using the point/slope form of a straight line `y-y_1=m(x-x_1)` the equation we seek is;

`y-(3/2)=(-1/4)(x-6)`
`:. y-3/2 = -1/4x+3/2`
`:. y = -1/4x+3`

Hence the equations of the two tangents that have gradient `-1/4` are (without loss of generality):

`l_1: \ \ \ y = -1/4x-3`
`l_2: \ \ \ y = -1/4x+3`

We can verify this graphically: