Question #cbfb8
1 Answer
There is one critical number, at
Explanation:
Start by finding the derivative by the power rule.
f'(x) = 3x^2 - 6x + 3
The critical points will occur when the derivative equals
0 = 3x^2 - 6x + 3
0 = 3(x^2 - 2x + 1)
0 = (x -1)(x - 1)
x = 1
Next, we must verify whether this is a local minimum or a local maximum. Note that this function will never have an absolute maximum/minimum, as shows the table below.
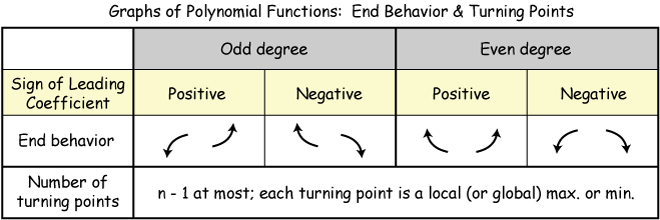
We can verify whether this point is a local min or a local max by finding the intervals of increase/decrease.
Test point 1:
f'(0) = 3(0)^2 - 6(0) + 3 = 3
Test point 2:
f'(3) = 3(3)^2 - 6(3) + 3 = 27 - 18 + 3 = 12
Since
Hopefully this helps!

