Question #aa149
1 Answer
Explanation:
First, set the equation equal to zero. Do this by subtracting the
#sinxtan^2x - sinx = 0#
Now, noticing that each term has at least one
#color(blue)(sinx)color(red)((tan^2x - 1)) = 0#
We have made it much easier to solve! Set each factor (whatever is being multiplied) equal to zero and solve.
#color(blue)(sin x) =0# ...and...#color(red)(tan^2x-1) = 0#
Let's being with the equation on the left.
#color(blue)(sin x) = 0#
Think back to the location on the unit circle where
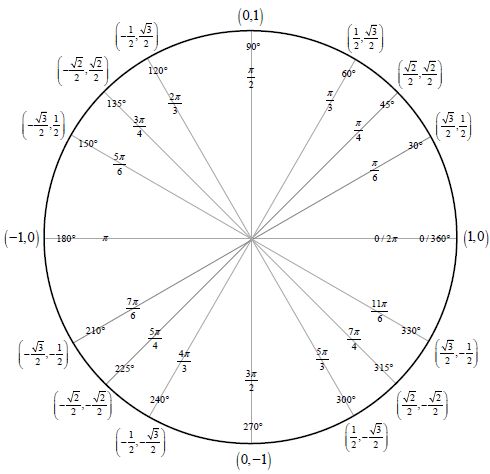
This happens when the radian value is
#color(blue)(x) = 0#
#color(blue)(x) = pi#
We have found two solutions for
#color(red)(tan^2x-1) = 0#
To solve, begin by isolating the
#color(red)(tan^2x) = 1#
Next we have to take the square root of both sides.
#color(red)(sqrt(tan^2x)) = sqrt(1)#
Since the square root of something squared is itself and the square root of
#color(red)(tanx) = 1# ...and...#color(red)(tanx) = -1#
At this point, we have to think back again to the unit circle. Since
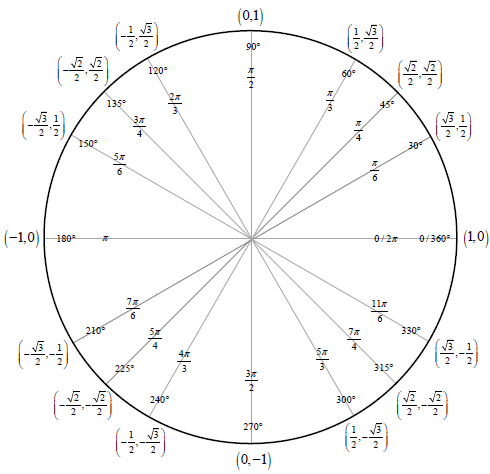
This is true when the radian value is
These are all of the solutions we found. Let's review our steps:
1.) Get all terms to one side and set the equation equal to zero.
2). Factor (doesn't work in every equation, but was useful here).
3). Set each factor equal to zero and solve using the unit circle.

