Question #6a5d5
1 Answer
The raising of the boiling point is one of the colligative properties of solutions.
Being a colligative property, the effect is independent of the identity of the solute, but only the amount of solute in solution.
The equation for boiling point elevation is
where
-
#DeltaT_b# is the change in boiling point (a positive quantity) of the solution -
#i# is the van't Hoff factor, which is essentially the number of dissolved ions per unit of solvent (assuming#"HCl"# is the solute, this value is#2# , because there is#1# #"H"^+# ion and#1# #"Cl"^-# ion per unit of#"HCl"# ) -
#m# is the molality of the solution;
#"molality" = "mol solute"/"kg solvent"# If we can figure out these two quantities, we can figure out the solution's molality.
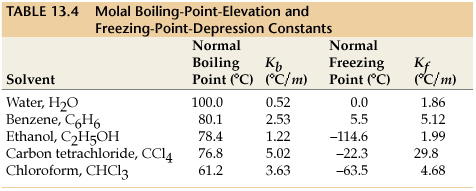
#K_b# is the molal boiling point elevation constant for the solvent (assumed to be benzene). We can find this value from a list online:
From this, we can see that
Plugging in the known values for the situation, we have
As long as we know the molal concentration
Let's say there is
The molality would be
Plugging this into the equation, we can find the boiling point elevation:
This quantity represents by how much the boiling point of the solvent (benzene) increases; to find the new boiling point of this solution, we simply add this to the normal boiling point of benzene (according to the above figure, it is
rounded to one decimal place.