Find the derivative of # x^2 + y^2 = (5x^2 + 4y^2 -x)^2 #, and find the equation of the tangent at #(0,0.25)#?
1 Answer
The derivative is given (implicitly) by;
# x + ydy/dx = (5x^2 + 4y^2 -x)(10x+8ydy/dx-1) #
The equation of the tangent at
# y = x + 1/4 #
Explanation:
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point.
When we differentiate
However, we cannot differentiate a non implicit function of
When this is done in situ it is known as implicit differentiation.
We have:
# x^2 + y^2 = (5x^2 + 4y^2 -x)^2 #
Differentiate wrt
# 2x+2ydy/dx = 2(5x^2 + 4y^2 -x)(10x+8ydy/dx-1) #
# :. x + ydy/dx = (5x^2 + 4y^2 -x)(10x+8ydy/dx-1) #
Whilst we could spend time and effort to find an explicit equation for
# => 0 + 1/4 dy/dx = (0 + 4(1/16) -0)(0+8/4dy/dx-1) #
# :. \ \ \ \ \ \ \ \ 1/4 dy/dx = (1/4)(2dy/dx-1) #
# :. \ \ \ \ \ \ \ \ 1/4 dy/dx = 1/2dy/dx-1/4 #
# :. \ \ \ \ \ \ \ \ 1/4 dy/dx = 1/4 #
# :. \ \ \ \ \ \ \ \ \ \ \ \ dy/dx = 1 #
So the tangent passes through
# \ \ \ \ \ y-1/4 = 1(x-0) #
# :. y-1/4 = x #
# :. \ \ \ \ \ \ \ \ y = x + 1/4 #
We can verify this solution graphically;
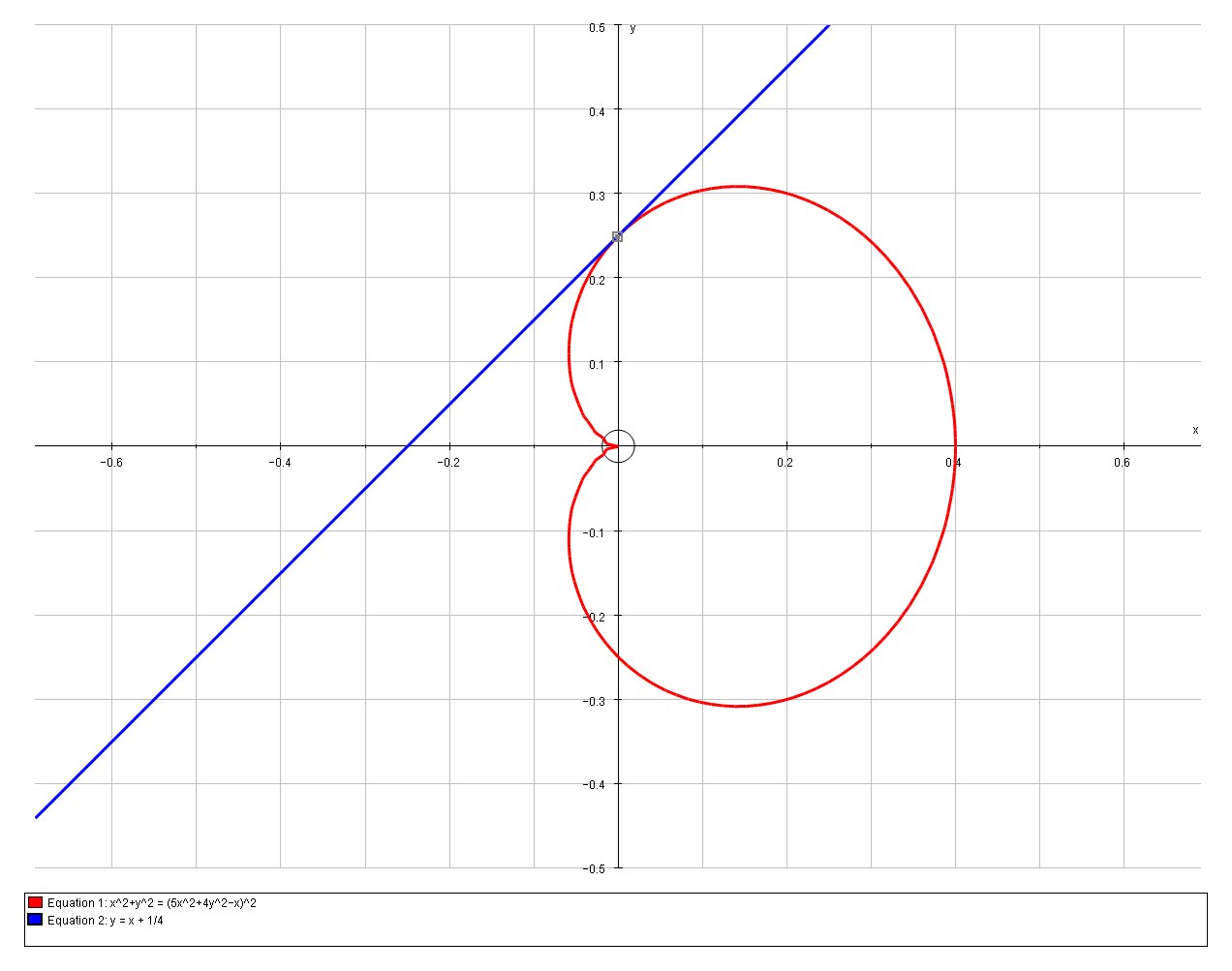
Advanced Calculus
There is another (often faster) approach using partial derivatives. Suppose we cannot find
# (partial F)/(partial x) (1) + (partial F)/(partial y) dy/dx = 0 => dy/dx = −((partial F)/(partial x)) / ((partial F)/(partial y)) #
So Let
#(partial F)/(partial x) = 2x - 2(5x^2 + 4y^2 -x)(10x-1)#
#(partial F)/(partial y) = 2y - 2(5x^2 + 4y^2 -x)(8y) #
And so:
# dy/dx = -(2x - 2(5x^2 + 4y^2 -x)(10x-1))/(2y - 2(5x^2 + 4y^2 -x)(8y))#
# \ \ \ \ \ \= -(x - (5x^2 + 4y^2 -x)(10x-1))/(y - 8y(5x^2 + 4y^2 -x))#
Here we get an immediate implicit function for the derivative, so again at
# dy/dx = -(0 - (0 + 4/16 -0)(0-1))/(1/4 - 8/4(0 + 4/16 -0))#
# \ \ \ \ \ \ = -(- (1/4)(-1))/(1/4 - 2(1/4))#
# \ \ \ \ \ \ = -(1/4)/(-1/4)#
# \ \ \ \ \ \ = 1 \ \ \ \ # , as before

