Question #da32c
2 Answers
Explanation:
To 'get rid' of the eighths power we need to take the 8th root.
Another approach would be to use binomial expansion. I am not going to do that.
The technique I am about to use crops up every now and then. So it is useful to know.
Note that the general case of
Also reversing the process of a log is written
In the 'old days' they were called an 'antilog'.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Divide both sides by 2
As a check: taking repeated square roots of 6 negating it and subtracting 8, I approximate the solution should be of the order:
-9.11849.......
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Taking logs of both sides
The difference between the two answers is:
Rounding errors in the calculator would contribute to the difference.
Only starting off the calculation using binomial expansion. Lot of work! You may continue on if you desire!! :-)
Good luck!
Explanation:
Consider only the
This one is basically a memory feat.
Standardised case going to use
In this case we start with
I am not going to write all that lot out!
Using Pascal's triangle we have:
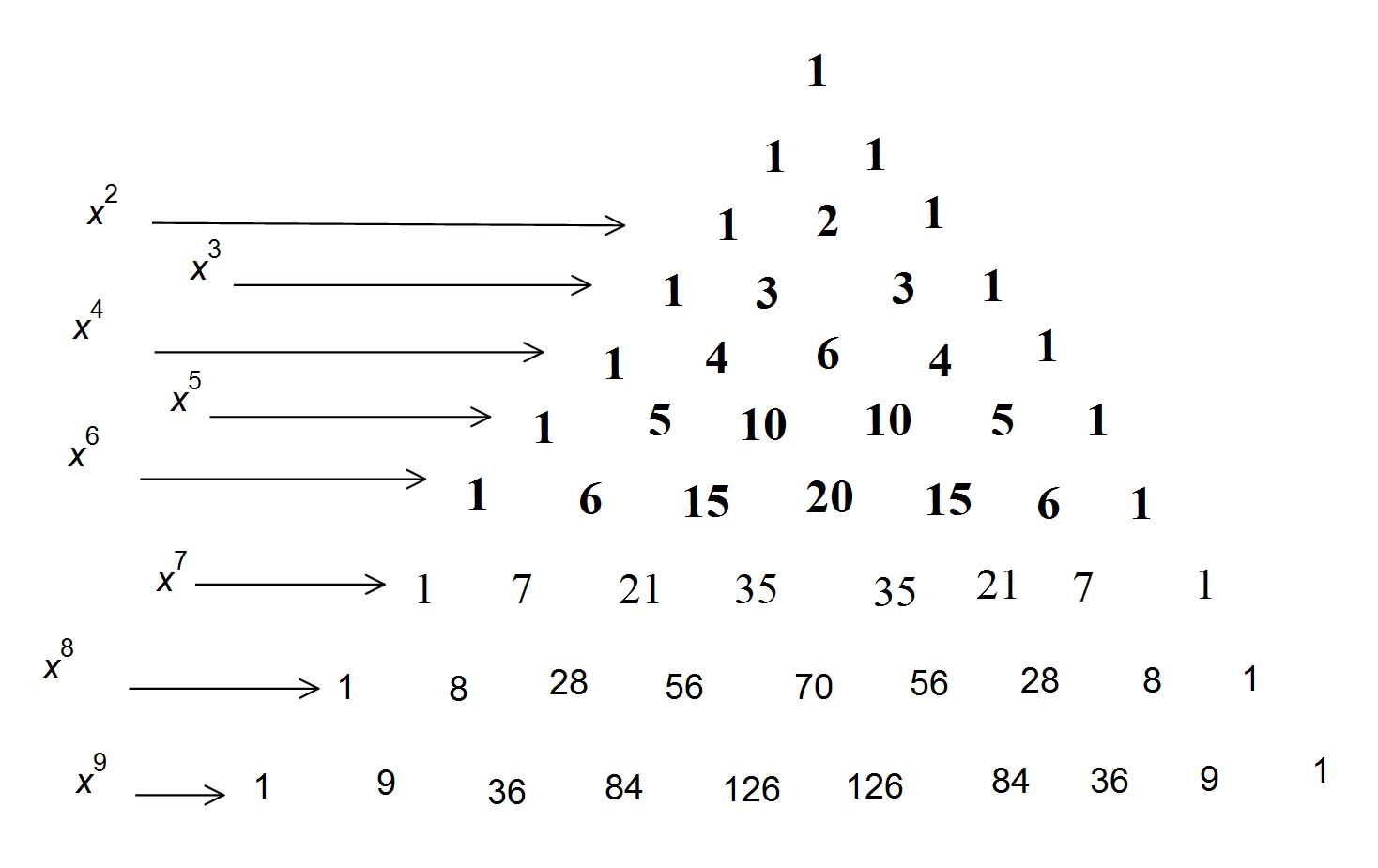
Now you substitute for

