Question

Explain why the entropy increased when the enzyme binds to the substrate? I thought binding to the substrate would reduce the entropy because it is more ordered?

Answer 1

The entropy you refer to is the entropy of activation, `DeltaS^(‡)`, which is a function of the temperature and volume of activation. So if the volume of activation has increased (due to substrate binding to enzyme), the entropy of activation has increased.

Or, upon binding to the enzyme, the enzyme disperses some energy outwards to the substrate (think delocalization and resonance), lowering the energy of the transition state (thereby decreasing the activation energy). This increased energy dispersal indicates greater entropy of activation.

---

Transition states can be modeled by the Eyring-Polanyi equation:

`k = (kappak_BT)/h "exp"(-DeltaG^(‡)//RT)`

where:

• `k` is the rate constant for a process.
• `kappa` is the transmission factor (i.e. the ratio of transmitted to reflected particles). Usually this is assumed to be `1`, saying that the transition state completely proceeds towards product.
• `k_B` is the Boltzmann constant.
• `T` is the temperature.
• `h` is Planck's constant.
• `DeltaG^(‡)` is the change in Gibbs' free energy of activation, `G^(‡) - G_R`, where `G_R` is the Gibbs' free energy of the reactants.
• `R` is the universal gas constant.

Using the isothermal Gibbs equation `DeltaG^(‡) = DeltaH^(‡) - TDeltaS^(‡)`, and assuming `kappa = 1`:

`k = (k_BT)/h "exp"(-(DeltaH^(‡))/(RT) + (DeltaS^(‡))/R)`

Upon rearranging, we get a linear form of the equation:

`barul|stackrel(" ")(" "ln k = -(DeltaH^(‡))/R 1/T + (DeltaS^(‡))/R + ln((k_BT)/h)" ")|`

Now, let's see what could happen to increase the rate constant, i.e. speed up the reaction.

• After the substrate binds onto the enzyme, the mechanism becomes more dissociative going away from the transition state, i.e. the volume of the transition state is larger than the volume of the reactants (`DeltaV^(‡) > 0`), and the substrate in the activated complex is going to break away from it soon.

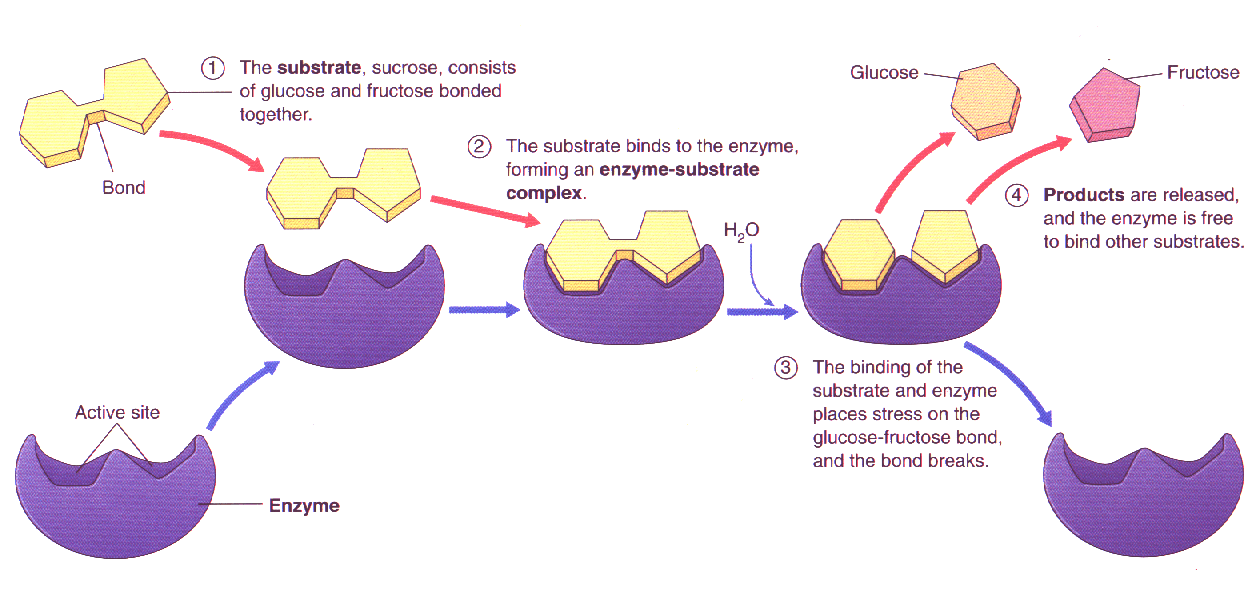
This increased dispersion of energy from within the enzyme outwards to the substrate makes `DeltaS^(‡) > 0`. The reaction proceeds on the enzyme more quickly now that the bonds in the reactant are more willing to break apart. That increases the rate.

• Decreasing `DeltaH^(‡)` should make sense.

When the enzyme binds (or anything, really), energy is released, so the enthalpy of activation is negative (`DeltaH^(‡) < 0`), thereby increasing the right-hand side of the equation, so `k` increases.

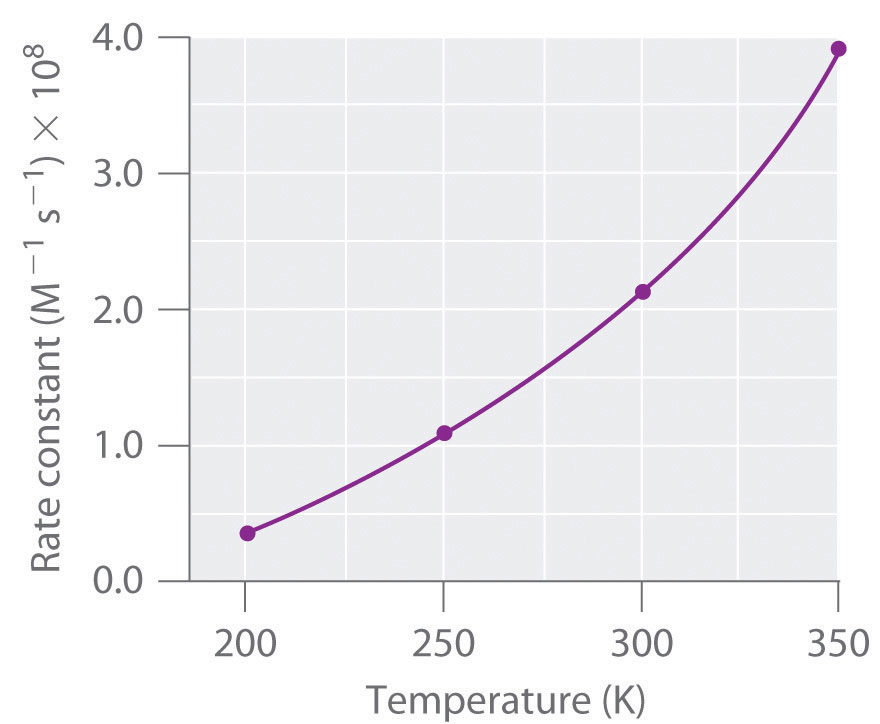
• In this case, we expect increasing `T` to increase `k`. That's pretty normal. Sometimes it may denature a protein, slowing that down... but if that isn't the case, then the rate increases.