Question #df22a
1 Answer
Feb 25, 2017
I got:
Explanation:
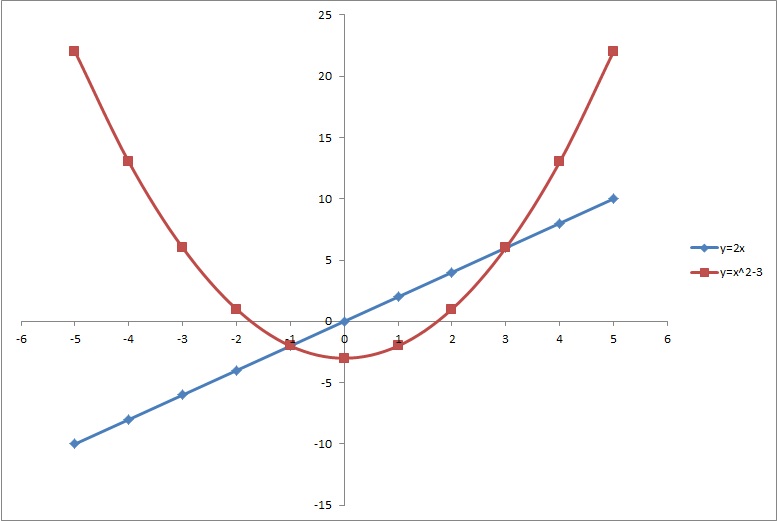
We can try substituting the first into the second equation for
solve using the Quadratic Formula:
we get two solutions:
These two values, substituted into the first equation will give us:
Graphically: