Question #b36f6
1 Answer
If the selected acid is weaker, the flatter part of the graph to the left of the equivalence point (where little pH change occurs) rises, as does the pH of the equivalence point.
Explanation:
The image below shows a typical titration curve for the addition of a strong base into a weak acid. Note that the equivalence point comes at a value somewhat greater than seven.
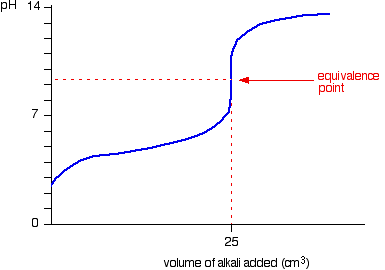
Two points on the graph are of interest. The first is called the half-equivalence point. (Sorry, it is not shown on the graph, but it lies midway from the pH axis to the equivalence point.) This is reached when the amount of base added in enough to change half of the acid into its conjugate base. At this point
(Check the
If one acid chosen is weaker than another, its
The second point of interest is, of course, the equivalence point. This comes at a point where the amount of added base matches the original amount of acid present. At this point, essentially all the HA has been ionized into
So, the calculation of the pH at the equivalence point is identical to the calculation of pH of a solution made by dissolving
So, to summarize, as the

