An exponential function passes through the points #(-3, 8)# and #(0, 1)#. What is the equation of the function?

Question

15614 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-03-02T00:22:53

The function has equation #y = (1/2)^x#.

It may look like you only have #1# point, but in fact you have #2#.

Every exponential function has its y-intercept at #(0, 1)#, because #n^0 = 1# for every real value of #n#.

We conclude the equation can be written in the form

#y = ab^x#

We can write a system of equations in two variables to solve for parameters #a# and #b#.

#{(8 = ab^-3), (1 = ab^0):}#

We can see by inspection, using the property #n^0 = 1#, that #a = 1#.

We can now readily solve for #b#.

#8 = 1(b^-3)#

#8 = b^-3#

#2^3 = b^-3#

#2^3 = 1/b^3#

#b^3 = 1/2^3#

#(b^(3))^(1/3) = (1/2^3)^(1/3)#

#b = 1/2#

The function therefore has equation #y = (1/2)^x#

Practice Exercises

a) It passes through the points #(2, 12)# and #(-1, 3/2)#.

b) The following graph:
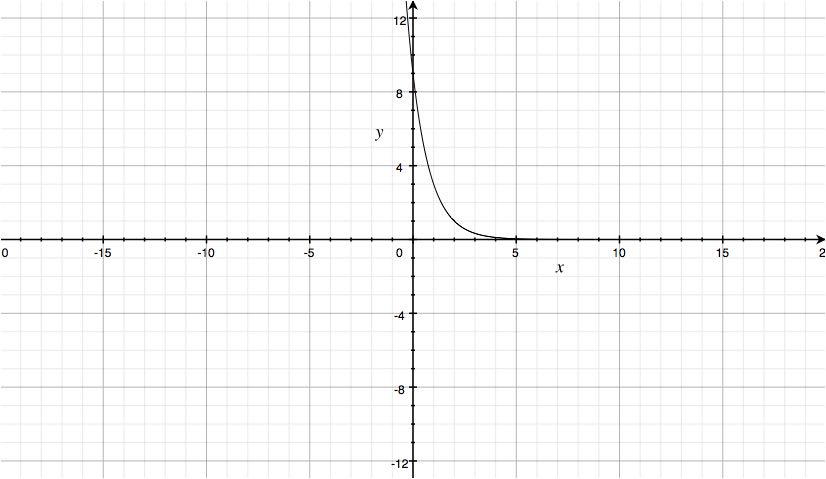
enter image source here

Solutions
1a) #y = 3(2)^x#
1b) #y = 9(1/3)^x#

Hopefully this helps!