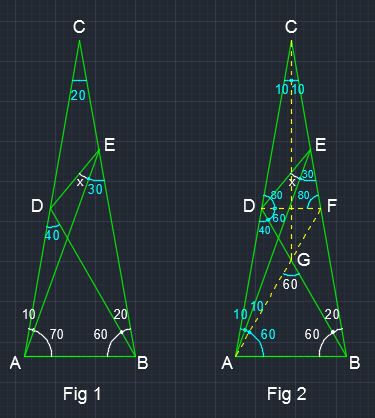
As shown in Fig 1,
#angleACB=180-(80+80)=20^@#
#angleADB=180-(80+60)=40^@#
#angleAEB=180-(70+80)=30^@#
As shown in Fig 2,
Draw a line #DF#, which is parallel to #AB#,
#=> angleEFD=angleCDF=80^@#
#=>angleFDB=60^@#
Draw a line #AF#
let #G# be the intersection point of #AF and BD#
#=> angleBAG=60, => angleAGB=60#
#=> angleDGF=60, => DeltaDGF# is equilateral.
#=> FG=GD=FD#
As #angleACF=angleCAF=20^@, DeltaCFA# is isosceles.
#=> CF=FA#
Draw a line #CG#, which bisects #angleACB#,
#=> DeltaACG and DeltaCAE# are congruent triangles. (they share one common side #AC# and their 3 corresponding angles are equal).
#=> AG=CE#
Since #CF=FA, and CE=AG, => FE=FG#
Since #FG=FD, => FE=FD, => DeltaFED# is isosceles.
#=> angleFED=x+30=1/2(180-80)=50#
#=> x=20^@#