Question #a5f60
1 Answer
Here's what I got.
Explanation:
!! VERY LONG ANSWER !!
As you know, we can use a set of four quantum numbers to describe the location and spin of an electron in an atom.
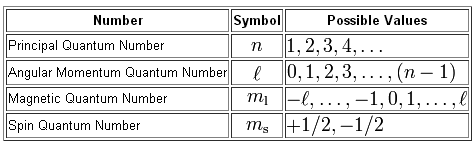
Your goal here is to figure out the maximum number of electrons that can share the incomplete sets of quantum numbers given to you.
Keep in mind that every complete set of quantum number is unique and can only belong to a single electron. In other words, no two electrons can have the same values for all four quantum numbers.
Before moving on, it's worth noting that
#{(n = "energy level"), (l = "subshell"), (m_l = "orbital"), (m_s = "spin") :}#
Also, keep in mind that each individual orbital can hold a maximum of
So, let's start looking at the incomplete sets given to you.
#color(blue)(ul(color(black)(n=3, m_l = -2)))#
In this case, you know that the electrons are located on the third energy level, i.e. in the third energy shell, because they have
Now,
#n = 3 implies l = {0, 1, 2}#
but only
#m_l = {-2, -1, 0, 1, 2}#
This means that the maximum number of electrons that can share these two quantum numbers is equal to
#color(darkgreen)(ul(color(black)(n=3, m_l = -2 implies "2 e"^(-)color(white)(.)"max")))#
#color(blue)(ul(color(black)(n=4, l = 3)))#
This time, you know that you're working on the fourth energy level because
In this case, the angular momentum quantum number can take the values
#l =0 -># the s subshell#l =1 -># the p subshell#l =2 -># the d subshell#l =3 -># the f subshell
This means that you must figure out the maximum number of electrons that can occupy the
#m_l = (-3, -2, -1, 0, 1, 2. 3}#
Since each value of
This means that the maximum number of electrons that can share these two quantum numbers is equal to
#7 color(red)(cancel(color(black)("orbitals"))) * ("2 e"^(-)color(white)(.)"max")/(1color(red)(cancel(color(black)("orbital")))) = "14 e"^(-)color(white)(.)"max"#
Therefore, you will have
#color(darkgreen)(ul(color(black)(n=4, l = 3 implies "14 e"^(-)color(white)(.)"max")))#
#color(blue)(ul(color(black)(n=5, l = 3, m_l = 2)))#
In this case, you know the energy level, the subshell, and the orbital, so you should be able to say without too much trouble that a maximum of
These electrons are located on the fifth energy level, in the
#color(darkgreen)(ul(color(black)(n=5, l = 3, m_l = 2 implies "2 e"^(-)color(white)(.)"max")))#
#color(blue)(ul(color(black)(n=4, l = 1, m_l = 0)))#
Once again, you are given the energy level, subshell, and orbital, so you can conclude that a maximum of
These electrons are located on the fourth energy level, in the
#color(darkgreen)(ul(color(black)(n=4, l = 1, m_l = 0 implies "2 e"^(-)color(white)(.)"max")))#

