Help with the following electrochem problems about standard cell potentials?
1 Answer
DISCLAIMER: LONG ANSWER!
We also assume that all the metals have the same oxidation state.
#a)# Recall that#DeltaG^@ = -nFE_"cell"^@# . When#DeltaG^@# is negative at#25^@ "C"# and#"1 atm"# , we say the reaction is spontaneous. (Note that in general it is not true, unless we are at STP.)The more negative
#DeltaG^@# , the more positive#E_"cell"^@# , and thus, the more spontaneous the reaction, i.e. it is easier to oxidize the element and it is higher up on the activity series.
We can tell that
#W# is more easily oxidized than#X# ,#X# than#Y# , and#Y# than#Z# , simply because they are in the negative terminal, which we assume is the anode. Focus on those.
#Z# is not oxidized at all in any of these cells, so it is at the bottom.Therefore,
#W > X > Y > Z# .
#b)# The positive electrode will have electrons flowing into it. That would, e.g. give
#M^(nu+)(aq) + nu e^(-) -> M(s)# That is, one would literally see metal forming at the positive electrode.
#c)# Since#DeltaG^@ = -nFE_"cell"^@# ,#E_"cell"^@# is thus a state function, and we can add it. Note, however, that#E_"cell"^@# does not scale with the stoichiometric coefficients.
#W(s) + cancel(X^(nu+)(aq)) -> W^(nu+)(aq) + cancel(X(s))#
#cancel(X(s)) + cancel(Y^(nu+)(aq)) -> cancel(X^(nu+)(aq)) + cancel(Y(s))#
#cancel(Y(s)) + Z^(nu+)(aq) -> cancel(Y^(nu+)(aq)) + Z(s)#
#"------------------------------------------------------"#
#W(s) + Z^(nu+)(aq) -> W^(nu+)(aq) + Z(s)# Therefore, we have that
#E_"cell"^@# for the#WZ# reaction is:
#color(blue)(E_"cell"^((WZ))) = E_"cell,1"^@ + E_"cell,2"^@ + E_"cell,3"^@#
#= (1.10 + 0.46 + 0.47)# #"V"# #=# #color(blue)("2.03 V")# This should make sense since
#W# is most easily/spontaneously oxidized relative to#Z# . Since#Z# is most easily reduced, it makes for the best oxidizing agent, and thus makes for the most spontaneous (most positive#E_"cell"^@# ) reaction at STP.
#a)# By definition,#"1 M"# concentrations at#"298.15 K"# and#"1 atm"# is used for#E_"cell"^@# measurements.
#b)# It can be seen from the activity series that zinc is more easily oxidized than silver. Standard reduction potentials are listed below.
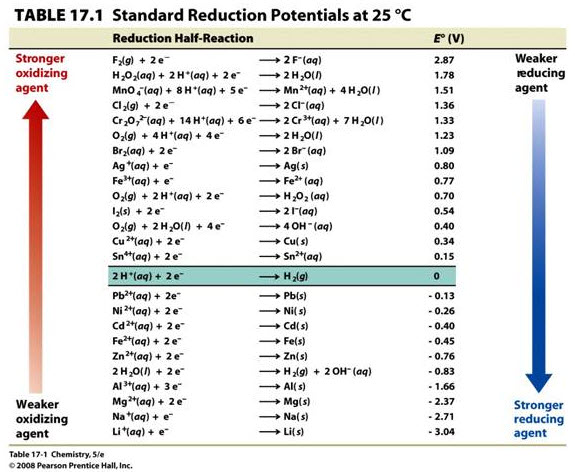
Read off of the table to find:
#E_"red,Zn"^@ = -"0.76 V"#
#E_"red,Ag"^@ = "0.80 V"# One way to calculate
#E_"cell"^@# is to identify that since zinc is more easily oxidized, flip its reduction reaction and flip the sign (#E_"ox"^@ = -E_"red"^@# ). Thus:
#color(blue)(E_"cell"^@) = E_"red"^@ + E_"ox"^@#
#= "0.80 V" + stackrel(E_"ox"^@)overbrace((-stackrel(E_"red"^@)overbrace((-"0.76 V")))) = color(blue)("1.56 V")# Again, stoichiometry does not affect
#E_"cell"^@# . This is still for the reaction
#"Zn"(s) + 2"Ag"^(+)(aq) -> "Zn"^(2+)(aq) + 2"Ag"(s)# .
#c)# I'm sure you can draw the arrow for the electron flow here. Since zinc is oxidized, electrons flow away from the zinc metal, i.e. to the right, from the negative to the positive electrode.
#d)# #"KCl"# is not used for the salt bridge because the ions are supposed to not participate in the reaction...#"Cl"^(-)# precipitates with... which ion?Look at your solubility rules and find that it is
#color(white)("Ag"^(+))# . When you figure it out, highlight this paragraph.
If you want to increase the cell potential, simply find an

