Question

Question #38d50

Answer 1

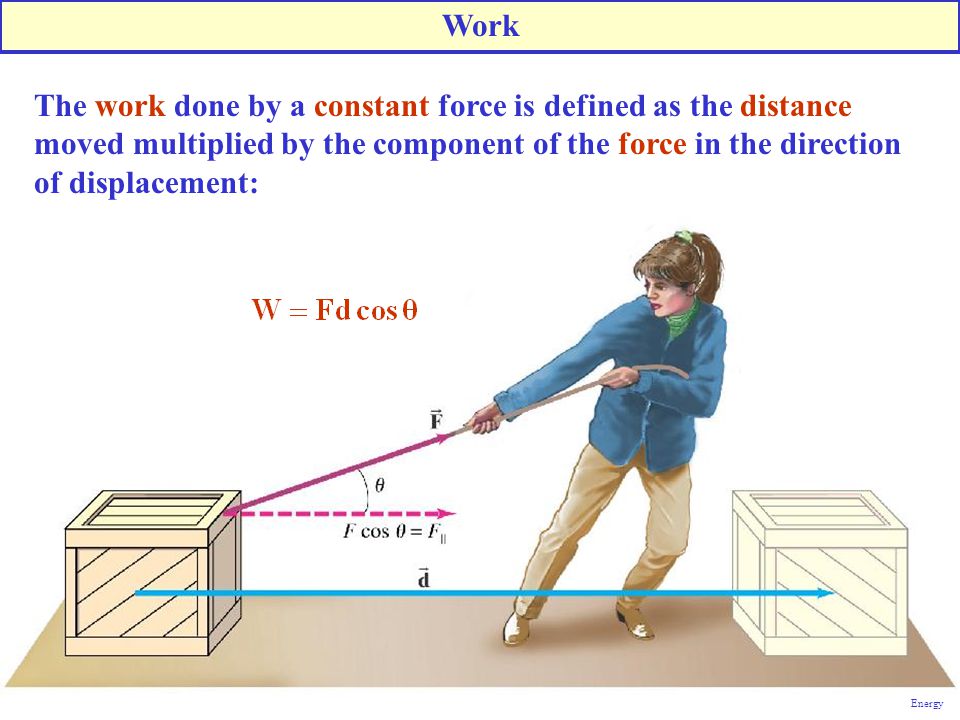
Following the definition of work written above we see that work done (W) by a constant force (`vecF`) is the product of the magnitude displacement (`vecd`) caused by it and the component of the force in the direction of displacement.

So mathematically

`W=abs(vecd) * abs(vecF)costheta`, where `theta` represents the angle between `vecF and vecd`

So vectorially

`W= vecF * vecd`

This means work is scalar product of two vectors quantities. So work is a scalar quantity.

TORQUE

When force is applied to rotate a body around an axis the magnitude of rotational effect caused by the force depends on three quantities (1) the distance of point of application of force from axis of rotation,the magnitude of radius vector (`absvecr`), (2) the magnitude of force `abs(vecF)` and (3) sine of the the angle `theta` between `vecF` and `vecr` and the product of these three quantities is the measure of the rotational effect caused and is known as torque

Mathematically

Magnitude of Torque

`tau =absvecrabsvecFsintheta`

So vectorially it is the cross product of two vectors `vecr and vecF` i.e.

`vectau=vecrxxvecF`

So torque is a vector quantity. The direction of torque is determined by the thumb rule as shown in above figure.