Question

A steel girder is taken to a 15ft wide corridor. At the end of the corridor there is a 90° turn, to a 9ft wide corridor. How long is the longest girder than can be turned in this corner?

Answer 1

Maximum girder length is `35.1` ft

Explanation:

Let us set up the following variables:

`{(x, "Partial distance along bottom",x+15=OA), (y, "total length along side",y=OB), (l, "Line Segment AB",l=AB),(alpha, angle " between AB and bottom",) :}`

All of `x`, `y` and `l` being strictly positive; `0 lt alpha lt pi/2`

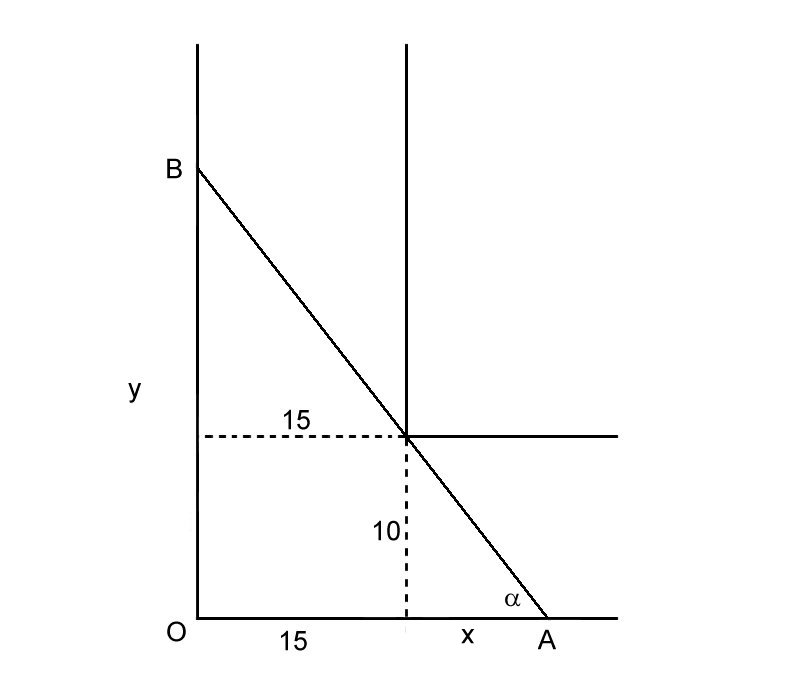
As the girder is moved through the corner of the corridor, it will get stuck if it is ever longer than the line segment `l=AB`. Therefore the longest girder that will go around the corner is length of the shortest line segment `AB`; therefore we should minimise `l`

METHOD 1

Our aim is to find `l(x)`, (a function of a single variable, `x`) and to minimize `l` wrt `x` (equally we could the same with `y` and we would get the same result). ie we want a critical point of `(dl)/dx`.

By Pythagoras:

`AB^2=OA^2+OB^2`
`:. l^2=(15+x)^2+y^2`

By similar triangles:

`OB : OA = 10 : x`
`:. y/(15+x) = 10/x`
`:. y = (10(15+x))/x`

Combining these results we get:

`:. l^2=(15+x)^2+((10(15+x))/x)^2`

By taking the (positive) square root we have achieved our goal of getting `l` a function of `x` alone. We want to minimize l, but equally we can minimize `L=l^2` to avoid needing to work with the square root; So:

`L = (15+x)^2 + (100(15+x)^2)/x^2`
`\ \ = (15+x)^2(1+100/x^2)`

Differentiating wrt `x` and plying the product rule we get:

`(dL)/dx = (15+x)^2(-200/x^3)+2(15+x)(1+100/x^2)`
`" " = (15+x){-200/x^3 (15+x) + 2(1+100/x^2) }`
`" " = (15+x)( -3000/x^3 - 200/x^2 + 2+200/x^2 )`
`" " = (15+x)(2 -3000/x^3 )`

At a max/min we have `(dL)/dx=0 => (15+x)(2 -3000/x^3 ) = 0`

Either `15+x = 0 = > x=-15`. But `x gt 0`
Or `\ \ \ \ \ \ 2 -3000/x^3 = 0 => 1500/x^3=1 => x=1500^(1/3)`

Thus we have:

`x = 11.44714 ...`
`L = 1233.2326...`
`l \ = 35.11741 ...`

I won't show that this is minimum (as required) but a plot or the second derivative test will show this is the case.

METHOD 2

We can also use a max/min method using trigonometry, considering the angle `alpha`, which invokes less algebra

From the large `Delta` we get;

`cos alpha = (15+x)/l`
`:. l = (15+x)/cos alpha`
`:. l = (15+x)sec alpha`

From the small `Delta` we get;

`tan alpha = 10/x`
`:. x = 10/tan alpha`
`:. x = 10cot alpha`

Combining these results we get:

`l = (15 + 10 cot alpha)sec alpha`
`\ = 15sec alpha + 10 cot alpha sec alpha`
`\ = 15sec alpha + 10 cos alpha /sin alpha 1/cos alpha`
`\ = 15sec alpha + 10 /sin alpha`
`\ = 15sec alpha + 10 csc alpha`

Differentiating `l` wrt `alpha` we get:

`(dl)/(d alpha) = 15sec alpha tan alpha - 10 csc alpha cot alpha`

At a max/min we have (dl)/(d alpha) #

`:. 15sec alpha tan alpha - 10 csc alpha cot alpha = 0`
`:. 3/(cos alpha) (sin alpha)/(cos alpha) = 2/(sin alpha) (cos alpha)/(sin alpha)`
`:. 3sin^3alpha=2cos^3alpha`
`:. tan^3alpha=2/3`

From which we get:

`alpha = 0.71802 ... ^c`
`alpha = 41.1398 ... ^o`
`l \ = 35.1174 ...`, as with Method 1