Question #f36b9
1 Answer
Jan 25, 2018
Refer explanation.
Explanation:
Given -
#y=x^4+8x^3#
To graph, a function, first find the turning points.
Find the first derivative and set it to zero, so that you know the value of
#dy/dx=4x^3+24x^2#
#dy/dx=0=>4x^3+24x^2=0#
#4x^2(x+6)=0#
#4x^2=0#
#x=0#
#x=-6#
At
Take a range of values that includes 0 and -6. Calculate the corresponding value of

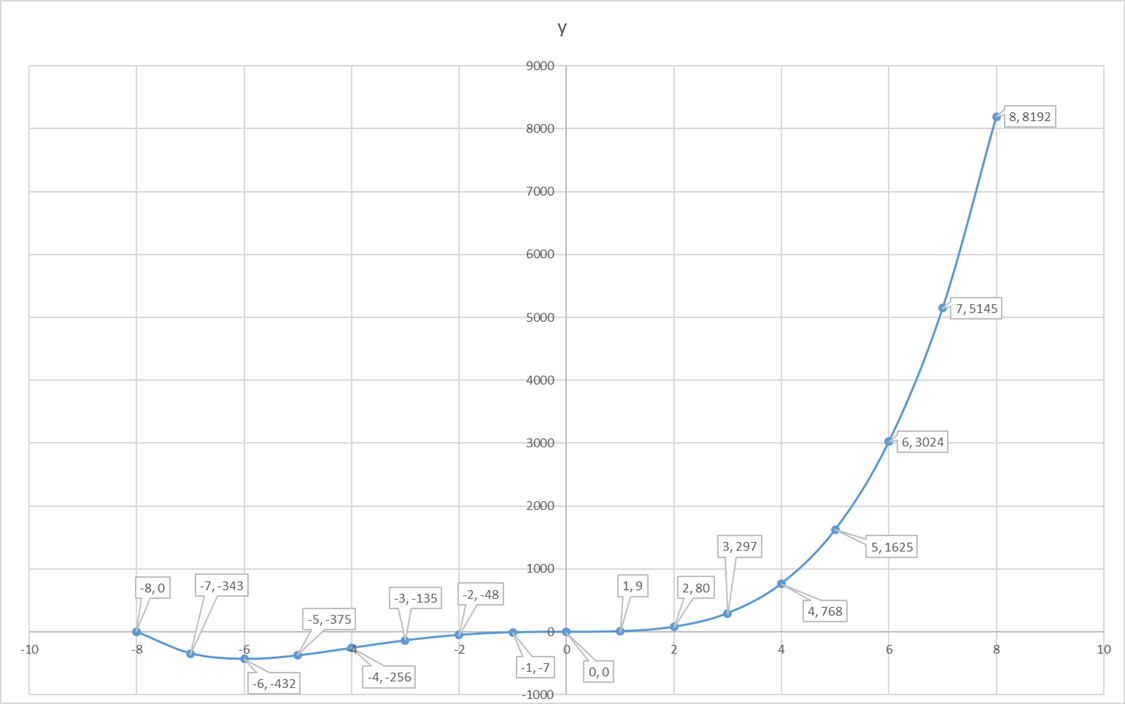
At
At

