Question

Question #ffc16

Answer 1

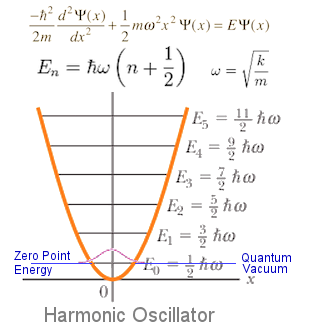
For a simple harmonic oscillator in one dimension, we have the following Hamiltonian:

`hatH = -ℏ^2/(2mu)(del^2)/(delx^2) + 1/2 kx^2 = -ℏ^2/(2mu)(del^2)/(delx^2) + 1/2 muomega^2x^2`

and the following energy (note that `ℏomega = h/(2pi)omega = hnu`):

`E_upsilon = ℏomega(upsilon+1/2) = hnu(upsilon+1/2)`

where `upsilon` is the vibrational quantum number, `nu` is the fundamental frequency, and `ℏ = h/(2pi)` is the reduced Planck's constant.

The zero-point energy is the energy at the bottom of the potential energy well, specifically at

`E_0 = hnu(0+1/2) = 1/2hnu = 1/2ℏomega`.

You were given that `k = "329 N/m"` or `"kg/s"^2`, so recall that the angular frequency is:

`omega = sqrt(k/mu)`

where `mu = (m_1m_2)/(m_1+m_2) = m/2` for `"Cl"_2`, `m` is the mass in `"kg"` (you must divide by `6.022 xx 10^(23)` to get its molar mass from `"kg/mol"` to `"kg"` if you use that), and `omega` is the angular frequency in `"s"^(-1)`.

Thus:

`color(blue)(E_0) = 1/2ℏomega = 1/2*1/(2pi)*hsqrt(k/mu)`

`= 1/(4pi)(6.626 xx 10^(-34) "J"cdot"s")sqrt("329 kg/s"^2/("0.03496885 kg/mol"/2 xx "1 mol"/(6.022 xx 10^(23) "molecules")))`

`= color(blue)(5.613 xx 10^(-21))` `color(blue)("J")`

or

`color(blue)("0.03504 eV")`

or

`color(blue)("282.59 cm"^(-1))`

A reference value from here is `"279.8756 cm"^(-1)` using only the simple harmonic oscillator approximation in the equation on pg. 392 in Table 2.