Question

Question #366ac

Answer 1

`X-C, W-D` are the alternate angle pairs

Explanation:

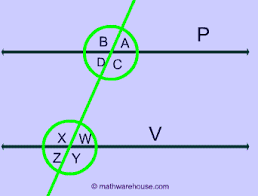
nswer: When a transversal cuts (or intersects) parallel lines several pairs of congruent and supplementary angles are formed.

Refer figure above

`X + D = 180` as they are supplementary, since lines P & V are parallel.

`X + W = 180` as they are supplementary.

That means `cancel(X) + D = cancel(X) + W`

`:. D = W` which are alternate angles.

`X-C, W-D` are the alternate angle pairs

`Z-D, X-B, Y-C, W-A` are the corresponding angle pairs

`Z-W, X-Y, A-D, B-C` are the vertically opposite angles pairs