.
This is the graph of #f(x)=sinx#:
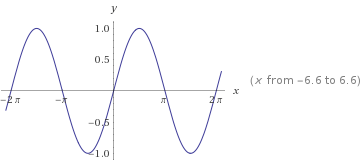
As you see, it has a period of #2pi# and amplitude of #1#..
This is the graph of #f(x)=sin2x#:
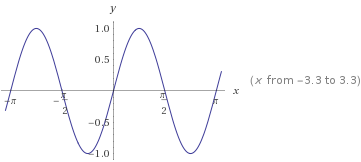
As you can see, it has a period of #pi# and amplitude of #1#. You have to divide the period of the sine function by the coefficient of your angle to get the period of your new function. In your problem, your angle is #x# and its coefficient is #2#. When you divide #2pi# by #2# you get #pi#.
Note that the amplitudes of both functions we graphed are #1#.
This is the graph of #f(x)=4sin2x#:
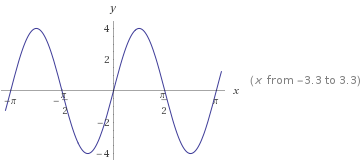
As you see, it has a period of #pi# and amplitude is #4# which tells you that if you have a coefficient behind the sine function, it gets multiplied by the amplitude of a normal sine function which is #1# and becomes the new amplitude, in this case #4#.
This is the graph of #f(x)=1+4sin2x#:
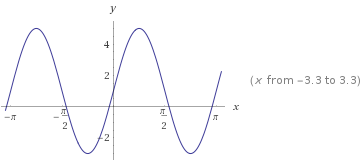
The constant that gets added to the function is the #y#-shift or vertical shift of the graph. In our problem, it is #+1#. This means that the graph of #f(x)=4sin2x# moves up by #1# unit in the #y# direction.
If you compare #4sin2x# with #1+4sin2x#, you will see that it has moved up one unit.
If you follow this process you can easily graph your trigonometric functions.





