Question

Question #81fd3

Answer 1

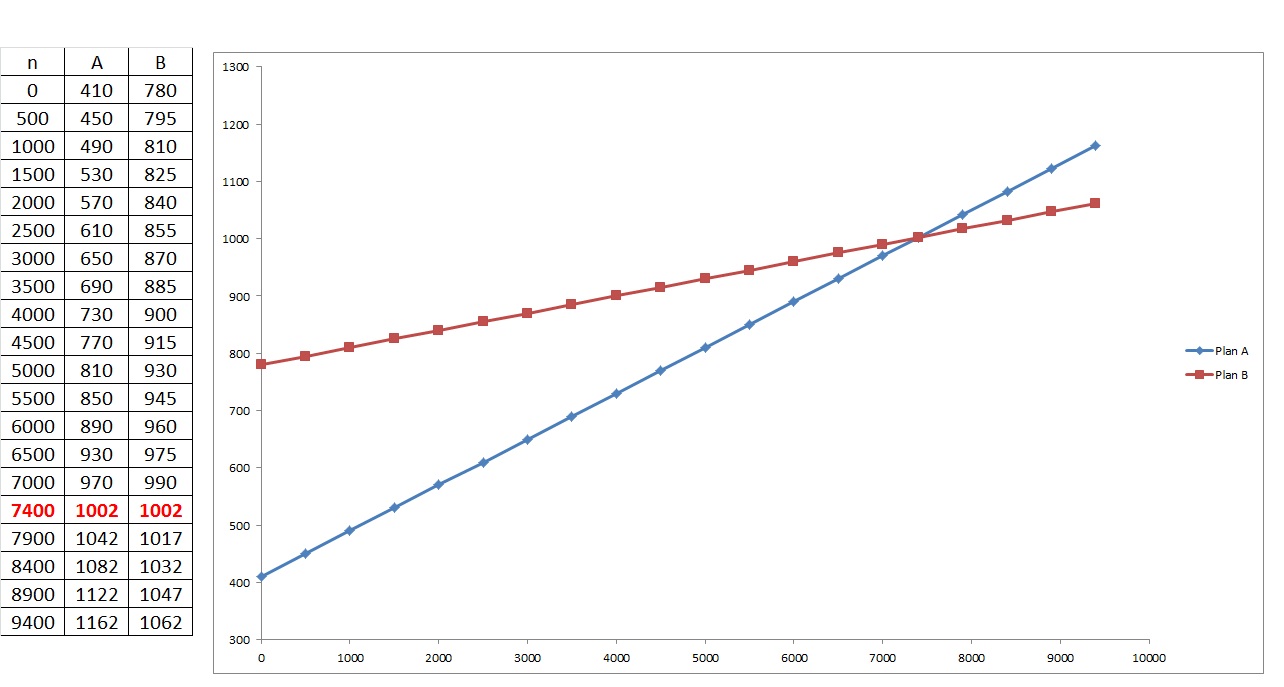
$7400/month or more.

Explanation:

This can be set up as two linear equations. What we want to know is the value of sales at which both equations are equal. Anything more than that would be the answer desired. We will set it up as a monthly amount, because that is what was given. A simple multiplication would give you an annualized amount.
Plan A: `(Total)_A = 410 + S*0.08`
Plan B: `(Total)_B = 780 + S*0.03`

Equivalence Point: `410 + S*0.08 = 780 + S*0.03`

`S*0.08 - S*0.03 = 780 – 410` ; `S*0.05 = 370` ; `S = 7400`

Answer 2

found for more than `$7400` sales.

Explanation:

I would represent the two plans using a linear function where the salary `s` will be function of the sales `n` as:
Plan A: `s_A=410+0.08n`
Plan B: `s_B=780+0.03n`
We can solve the equations together imposing `s_A=s_B` or:
`410+0.08n=780+0.03n`
`0.05n=370`
`n=$7400`

We can also plot both equations using for example Excel (but also by hand is perfectly feasible) to see the point when plan A becomes more interesting (value of sales on the `x` axis):