I'm assuming the physical set up looks like this:
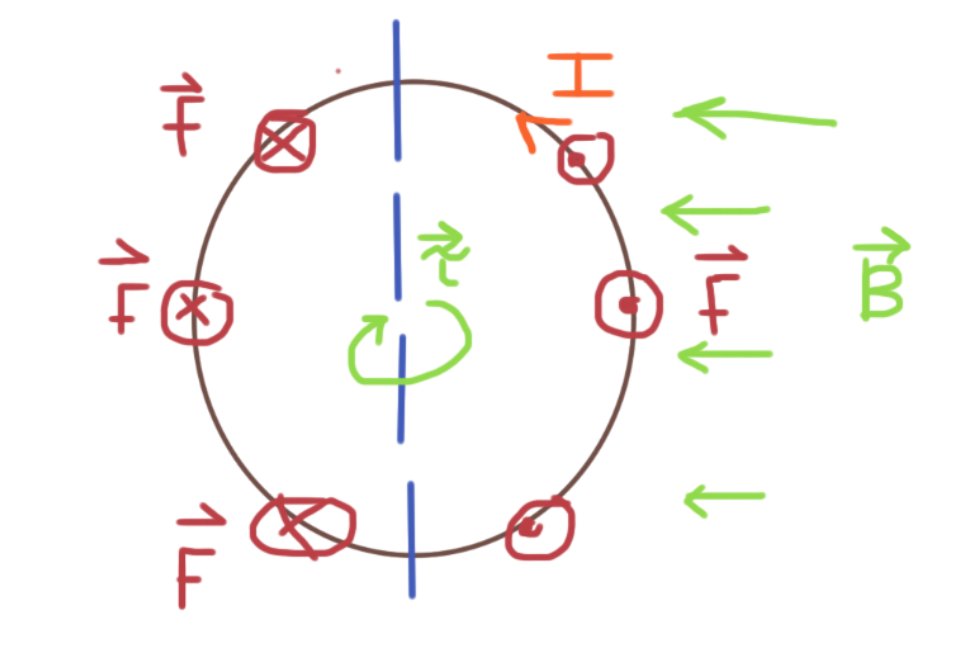
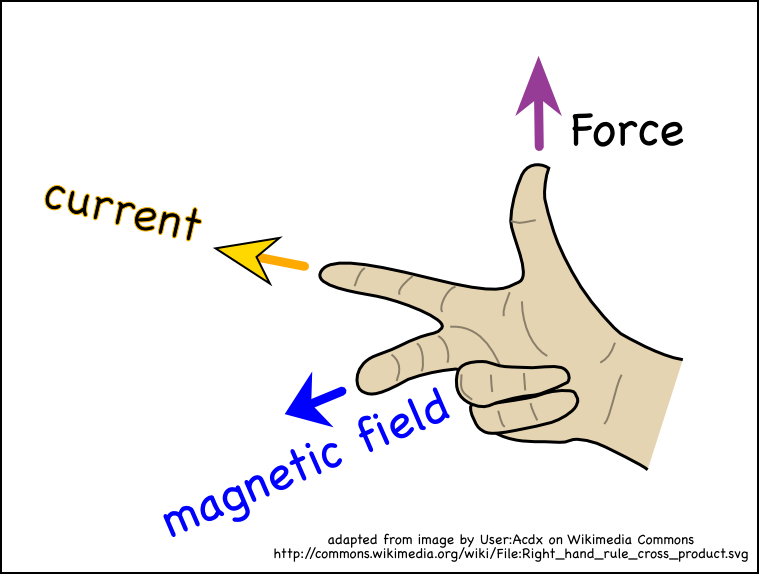
Assuming the current, #I#, is moving CCW as indicated, then the effect of the B field, again acting in the direction shown, will be to create a torque #vec tau# that spins the loop about it's axis as shown. In this set-up, from the right hand rule, the force vectors on the RHS of the blue vertical axis will act out of the page, and vice versa:
So we do that calculus thing and linearise a small element of the circular loop:
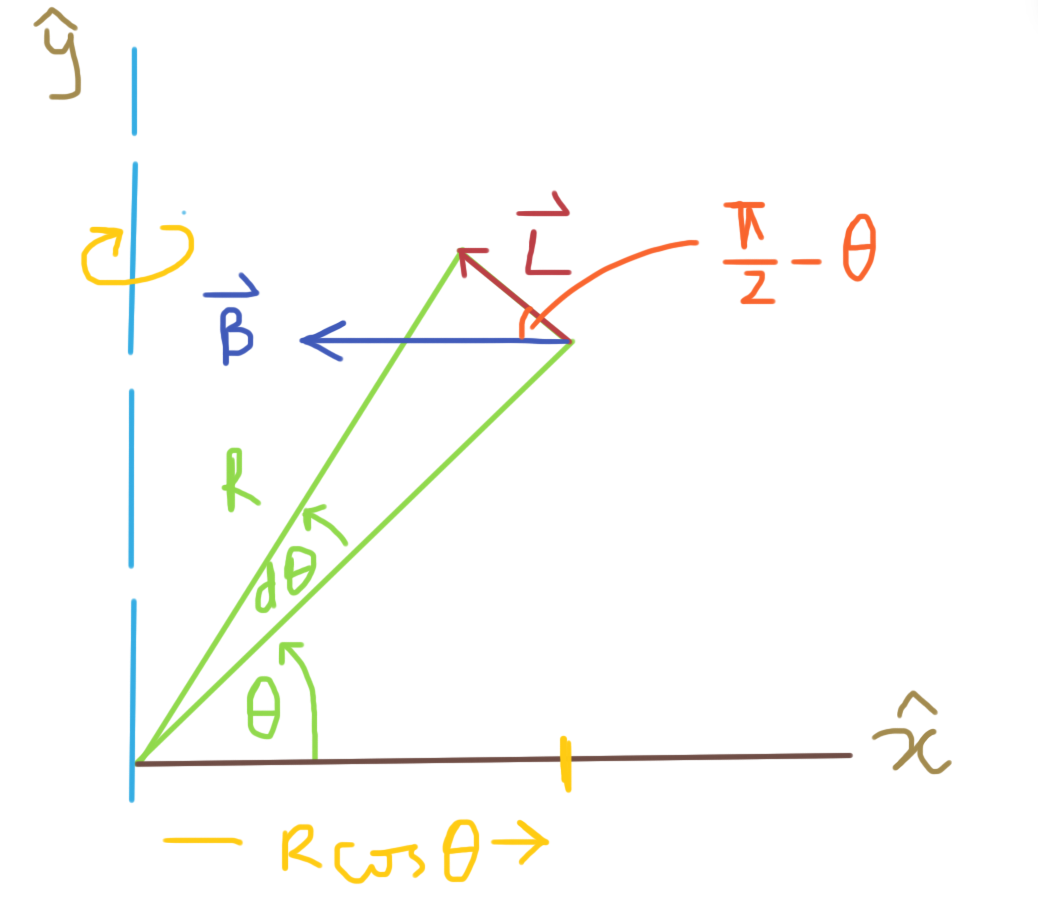
The force #vec F # on a current-carrying wire of length and orientation #vec L#, due to a magnetic field #vec B# (BTW this is all derived from the Lorentz Force Law), is:
#vec F = I (vec L xx vec B) #
From the drawing: #abs(vec L) = R d theta#
So, again from the right hand rule, the force #d vec F# on this small element is:
#d vec F = I abs(vec L) abs(vec B) sin (pi/2 - theta) \ hat z#, i.e. acting out of the screen/page.
# = I \ R \ d theta \ B \ cos theta \ hat z#
The associated torque #d vec tau# is:
#d vec tau = vec r xx d vec F#, where #vec r# is the small element's position vector relative to its axis of rotation .
In this case: #vec r = R cos theta \ hat x#
And so:
#d vec tau = R cos theta \ hat x xx I \ R \ d theta \ B \ cos theta \ hat z#
# = - IBR^2 cos^2 theta \ d theta \ hat y#
#implies vec tau = - IBR^2 int_0^(2 pi) cos^2 theta \ d theta \ hat y#
Simple maths sub and...
# = - pi IBR^2 \ hat y#
That means that:
#implies abs(vec tau) = pi IBR^2 #
#= pi (28 xx 10^(-3))( 0.9) (1.3/2)^2 = 0.033 Nm#




