Torque

Key Questions

  • What units is torque measured in?

    Answer:

    N.m
    Or
    #kgm^2sec^-2#

    Explanation:

    Torque = Force # xx# Distance

    Force is measured in newton and the distance is measured in meters

    so,

    Torque will be measured in newton #*# meter

    Newton #=kgmsec^-2#

    =#kgmsec^-2*m=kgm^2sec^-2#

    Yahia M. · 1 · Apr 22 2018
  • How can torque be calculated?

    Torque, or a moment, is defined as the cross product between a force and the position of that force relative to a given point. The torque formula is:

    #t = r * F#

    Where #r# is the position vector from the point to the force, #F# is the force vector, and #t# is the resultant torque vector. Because torque involves multiplying a position and a force together, its units will be either Nm (Newton-meters) or ft-lbs (foot-pounds).

    In a two-dimensional setting, torque is simply give as the product between a force and a position vector which is perpendicular to the force. (Or also the component of a force vector perpendicular to a given force vector).

    You will often see a torque specification recorded on truck commercials because it reflects the ability of the engine to transfer rotational motion into linear motion. (Drive shaft turns the axles of the car).

    Walker P · · Jul 1 2014
  • How can torque be increased?

    By increasing the perpendicular distance between forces or by increasing the magnitude of the perpendicular component of the forces.

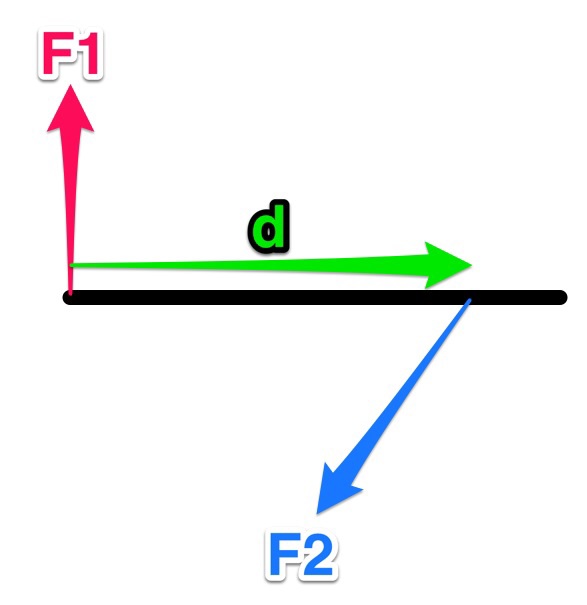
    enter image source here

    In this example there are two forces, F1 and F2. F2 is not perpendicular to the beam so only the perpendicular component (vertical in this case) will cause the beam to rotate. To increase the torque on the beam in this case the following can be done:

    1. Increase force F1.
    2. Increase force F2, or just increase the vertical component of F2.
    3. Increase d.
    Daniel W. · · Jun 23 2014
  • What is torque?

    Answer:

    Torque is the rotational analogue of force. It is the equivalent of force which makes a body rotate about some axis.

    Explanation:

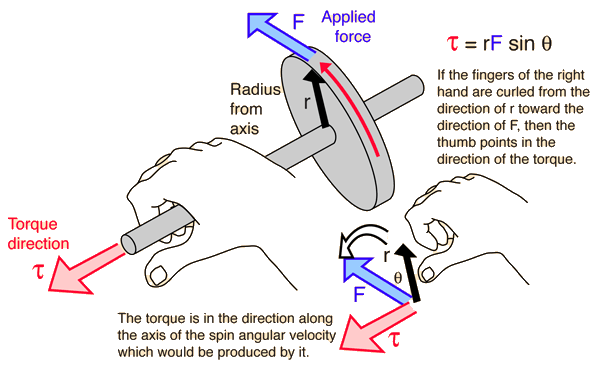
    enter image source here

    As you may see, it's the equivalent of force which makes the nut rotate about it's axis.

    Mathematically, Torque, #tau = r*F*Sin theta#, where #r# is the length of the rotating arm, #F# is the force and #theta# is the angle between the two.

    Torque is a vector, i.e. it has a direction associated with it. It is the cross product of vectors #vec r# and #vec F#.

    Image : hyperphysics.phy-astr.gsu.edu

    Aritra G. · 1 · Jun 5 2016

Questions

Rotational Motion