Question

A Sphere of radius `2a` has a hole of radius `a` drilled through the centre. What is the remaining volume?

Answer 1

`V = 4pisqrt3a^3`

Explanation:

Consider the section of the solid with a plane containing the axis of the cylinder and establish a system of reference with origin in the center of the sphere and with the axis of the cylinder as `x` axis.

The volume of the remaining solid is generated by the rotation around this axis of the area delimited by the semi circle or radius `2a` and the line `y=a`.

For reasons of symmetry this is twice the volume of the area of the first quadrant comprised between the quarter circle of radius `2a`, whose equation is `y = sqrt((2a)^2-x^2)` and the line `y=a`.

The two curves intercept when:

`a = sqrt((2a)^2-x^2)`

`a^2 = 4a^2-x^2`

`x= sqrt3 a`

The volume generated by the rotation of the area between `x` and `x+dx` is then:

`dV= pi (4a^2-x^2 -a^2) = pi( 3a^2-x^2)`

and integrating over the interval `(0, sqrt3 a)`:

`V = 2 int_0^(sqrt3 a) pi( 3a^2-x^2dx)`

`V= 2pi [3a^2x -x^3/3]_0^(sqrt3a)`

`V = 2pi (3sqrt3a^3- 3sqrt3a^3/3) =4pisqrt3a^3`

We can also calculate this geometrically, since the volume of the remaining solid is the volume of the sphere `V_s`, minus the volume of the cylinder `V_c`, minus the volume of the two spherical caps `V_p`:

`V=V_s-V_c-2V_p`

Now:

`V_s = 4/3pi(2a)^3= 32/3pia^3`

The height of the spherical caps is given by the formula:

`h= 2a-sqrt((2a)^2-a^2) = (2-sqrt(3))a`

and their volume is:

`V_p = pih/6(3a^2+h^2) = pi/6(2-sqrt(3))a(3a^2+((2-sqrt(3))a)^2) = (pia^3)/6(2-sqrt(3))(3+4-4sqrt3+3) = (pia^3)/6(2-sqrt(3))(10-4sqrt3)=(pia^3)/6(32-18sqrt3)`

The heigth of the cylinder is the diameter of the sphere minus the height of the caps:

`h_c = 4a - 2 (2-sqrt(3))a = a (4-4+2sqrt3) =2asqrt3`

so its volume is:

`V= pia^2h_c = 2pia^3sqrt3`

and finally:

`V=32/3pia^3-2pia^3sqrt3-2(pia^3)/6(32-18sqrt3)`

`V=pia^3(32/3-2sqrt3-1/3(32-18sqrt3))`

`V=pia^3/3(32-6sqrt3-32+18sqrt3)`

`V=pia^3/3(12sqrt3)`

`V=4pia^3sqrt3`

Answer 2

`4sqrt(3)pia^3`

Explanation:

We basically are being asked to calculate the volume of a spherical bead, that is, a sphere with a hole drilled through it.

Consider a cross section through the sphere, which we have centred on the origin of a Cartesian coordinate system:

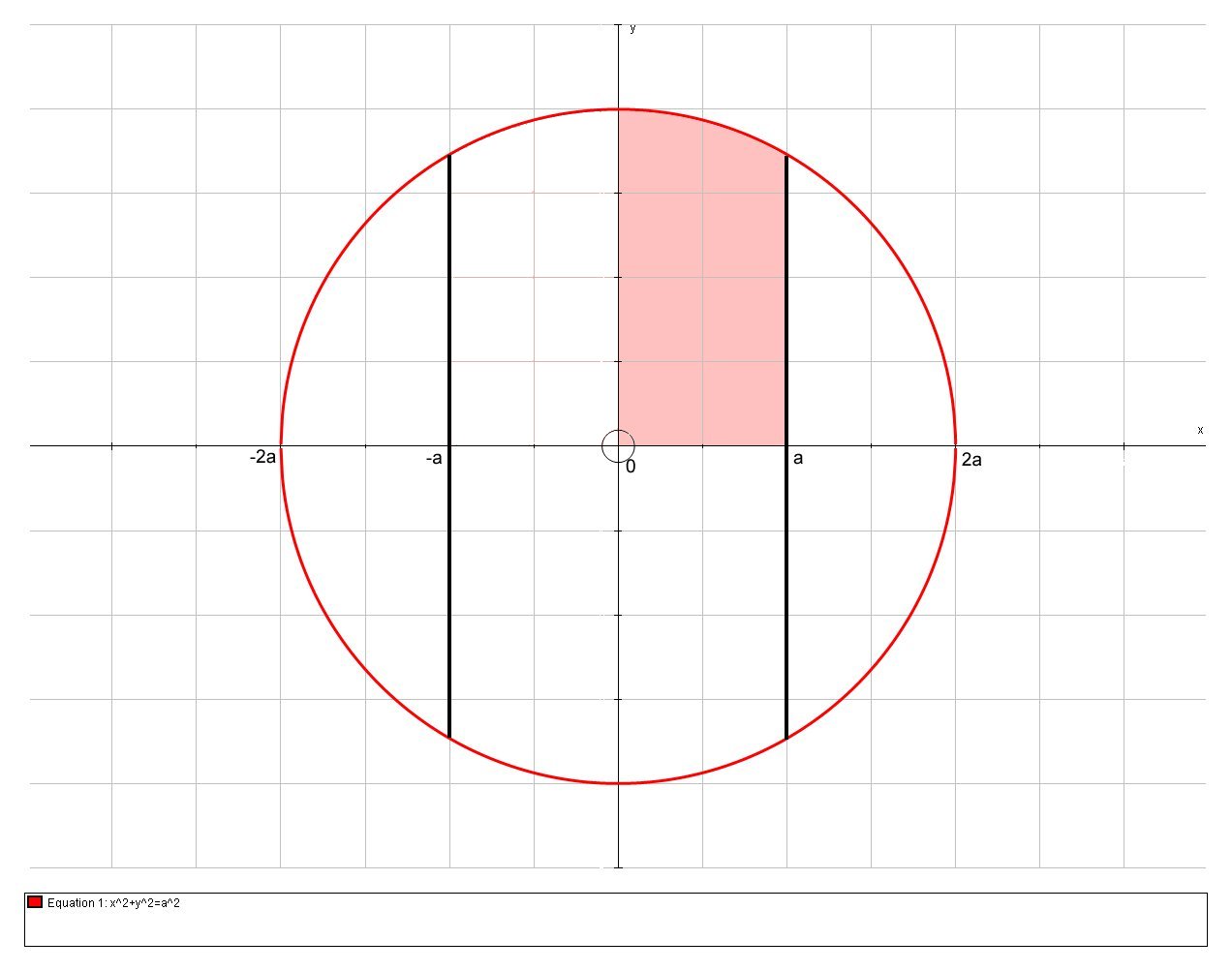
The red circle has radius `2a`, hence its equation is:

`x^2+y^2=(2a)^2 => x^2+y^2=4a^2`

Method 1 - Calculate core and subtract from Sphere

First let us consider the volume of the entire Sphere, which has radius `2a`. I will use the standard volume formula `V=4/3pir^3`

`:. V_("sphere") = 4/3 pi (2a)^3`
`" " = 4/3 pi 8a^3`
`" " = 32/3 pi a^3`

For the bore we can consider a solid of revolution. (Note this is not a cylinder as it has a curved top and bottom from the sphere). We will use the method of cylindrical shells and rotate about `Oy`, the shell formula is:

`V = 2pi \ int_(alpha)^(beta) \ xf(x) \ dx`

Also note that we require twice the volume because we have a portion above and below the `x`-axis. The shell volume of revolution about `Oy` for the bore is given by:

`V_("bore") = 2pi \ int_(0)^(a) \ x(2sqrt(4a^2-x^2)) \ dx`
`" " = 2pi \ int_(0)^(a) \ 2x \ sqrt(4a^2-x^2) \ dx`

We can evaluate using a substitution:

Let `u=4a^2-x^2 => (du)/dx = -2x`
When `{ (x=0), (x=a) :} => { (u=4a^2), (u=3a^2) :}`

And so:

`V_("bore") = -2pi \ int_(4a^2)^(3a^2) \sqrt(u) \ du`
`" " = 2pi \ int_(3a^2)^(4a^2) \sqrt(u) \ du`
`" " = 2pi \ [ u^(3/2)/(3/2) ] _(3a^2)^(4a^2)`

`" " = (4pi)/3 \ [ u^(3/2) ] _(3a^2)^(4a^2)`
`" " = (4pi)/3 \ ((4a^2)^(3/2) - (3a^2)^(3/2))`
`" " = 4/3pi \ (8a^3-3sqrt(3)a^3)`
`" " = 32/3pi a^3-4sqrt(3)pia^3`

And so the total volume is given by:

`V_("total") = V_("sphere") - V_("bore"`
`" " = 32/3 pi a^3 - (32/3pi a^3-4sqrt(3)pia^3)`
`" " = 4sqrt(3)pia^3`

Method 2 - Calculate volume of bead directly

We can use the same method of a solid of revolution using the method of cylindrical shells and rotate about `Oy`, but this time we will consider the bead itself rather than the core that is removed, again we need to twice the volume because we have a portion above and below the `x`-axis. The shell volume of revolution about `Oy` for the bead is given by:

`V_("total") = 2pi \ int_(a)^(2a) \ x(2sqrt(4a^2-x^2)) \ dx`
`" " = 2pi \ int_(a)^(2a) \ 2x \ sqrt(4a^2-x^2) \ dx`

We can evaluate using a substitution:

Let `u=4a^2-x^2 => (du)/dx = -2x`
When `{ (x=a), (x=2a) :} => { (u=3a^2), (u=0) :}`

And so:

`V_("total") = -2pi \ int_(3a^2)^(0) \sqrt(u) \ du`
`" " = 2pi \ int_(0)^(3a^2) \sqrt(u) \ du`
`" " = 2pi \ [ u^(3/2)/(3/2) ] _(0)^(3a^2)`

`" " = (4pi)/3 \ [ u^(3/2) ] _(0)^(3a^2)`
`" " = (4pi)/3 \ ((3a^2)^(3/2) - 0)`
`" " = (4pi)/3 \ (3sqrt(3)a^3 )`
`" " = 4sqrt(3)pia^3`, as above