Question

Question #cb21d

Answer 1

`F = 14.38 N`

Explanation:

I am assuming you are NOT asking for the net force on 1 charge and just the force due to one charge on the other. If so,

Coulomb's law describes the force between two point charges. It is calculated by using the following equation.

`color(white)(aaaaaaaaaaaaaaaa)` `F = (k*q_1*q_2)/r^2`

Where
`k = "Coulomb's law constant" (9.0 * 10^9 N*m^2/C^2)`
`q_1 = "point charge" (C)`
`q_2 = "point charge" (C)`
`r = "distance between the 2 point charges" (m)`

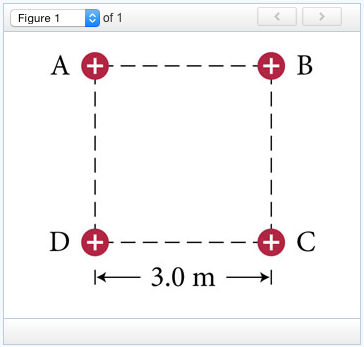
In the question stem, all four of the point charges have the same magnitude and all are positive. Since we know that "opposites attract", all four of the point charges would experience a repulsive force due to the other 3 charges.

If we were to calculate the Coulombic force on one of the charges due to another:

`F = (k*q_1*q_2)/r^2`
`F=((9.0 * 10^9 N*m^2/cancelC^2) * (+1.6*10^-5cancelC) * (+1.6*10^-5cancelC))/(0.4m)^2`
`F = (2.3N*cancelm^2)/(0.16cancelm^2)`

`F = +14.38 N`

A (+) Force indicates repulsion while a (-) Force indicates attraction . Since our charges are positive, the Force is repulsive.

`color(white)(aaaaaaaaaaaaaaaa)`

If we take a quick look at the figure below, if I were to calculate the `color(red)("force of B on A")` and the `color(blue)("force of A on B")`, the magnitude of the forces would be the same but their directions would be different since they would repel each other and move away from each other in opposite directions, assuming no other charges are around.