Question #edfff
1 Answer
Any object that is accelerating.
Explanation:
A good example is a ball falling. Another example is an object on an inclined plane that is falling down the slope:
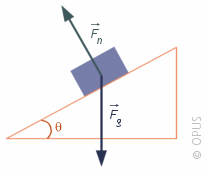
The picture above is not perfect because it's not showing the case of an object with a friction force. Because the object on an inclined plane could be stationary if the frictional force = downward force and so the forces would be balanced. It's important to know if there is some.
To be unbalanced the sum of the forces in all of these situations have to be not equal to 0. (
A great way to verify this, is to sum up all the forces in the two axes:
And then verify for each axes if it's equal to 0.
(
If in one of them it's not, you have an object with unbalanced forces!


