Question

Question #5da9f

Answer 1

We use the normalised Boltzmann distribution in multiple dimensions to find the Maxwell-Boltzmann distribution.

Explanation:

The distribution of molecular speeds is based on the Boltzmann weight of translational motions and gives the probability of finding a particle with a certain velocity.

Under thermal equilibrium conditions, the probability `p(E)` to find a particle in a certain state is inversely proportional to the exponential of the energy `E`, associated with that state taken relative to the energy associated with the present temperature, `k_"B" T`, often referred to as the thermal energy.

The normalised Boltzmann distribution is stated as following:
`f(v_"x")dv_"x"=(m/(2*pi*k"B"*T))^(1/2)*e^((-mv_"x" ^"2")/(2K_"B"T))dv_x`

This function gives the probability of finding a particle with a certain velocity in a certain direction. Here I chose to find only the particles with velocity `v` in the `x` direction, denoted as `v_x`.

Now we now that particles can move in three dimensions, not just in one. Therefore we need to find the distribution of speeds instead of the distribution of velocity.
Remember that the speed is the magnitude of the velocity vector.

The speed can, therefore, be calculated as:
`v=|vec v| = (v_"x" ^2 +v_(y)^2 +v_(z)^2)^(1/2)`

Now using that the probability is proportional to the exponential of `E`, we obtain:

`f(v) prop e^((-mv_"x" ^"2")/(2K_"B"T))`

`= e^((-mv_"x" ^2 +v_(y)^2 +v_(z)^2 )/(2K_"B"T))`
`=e^((-mv_"x" ^"2")/(2K_"B"T))+e^((-mv_"y" ^"2")/(2K_"B"T))+e^((-mv_"z" ^"2")/(2K_"B"T)) prop f(v_x)*f(v_y)*f(v_z)`

Then we combine them and obtain the Maxwell-Boltzmann distribution of molecular speeds is therefore given by:

`F(v)dv=4pi v^2 *(m/(2 pi K_"B" t))^(3/2) *e^((-mv^"2")/(2K_"B"T)dv`

And as you can see in this equation we write `v`, without the dimension notation (no x, y or z).
This equation gives the probability of finding a molecule with mass `m` with a speed between `v` and `v+dv` at absolute temperature T in a system at thermal equilibrium.

If you plot this function you get

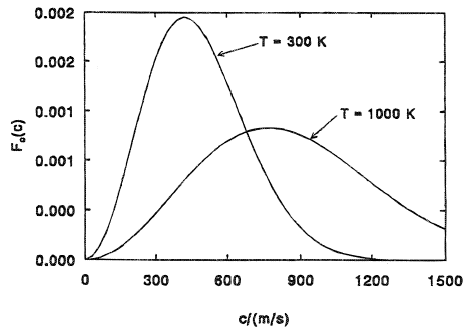
With the probability on the vertical axis and the speed of the particle on the horizontal axis.