Question #64787
1 Answer
Alrighty
Explanation:
I will walk you through two methods for HF (because typing is a pain :)). The first method will be your ICE table, which is the tougher approach, because, if you follow all the conventions, you have to do plenty of extra steps. The second one is the conventional way of doing this...
Enjoy
ICE Table
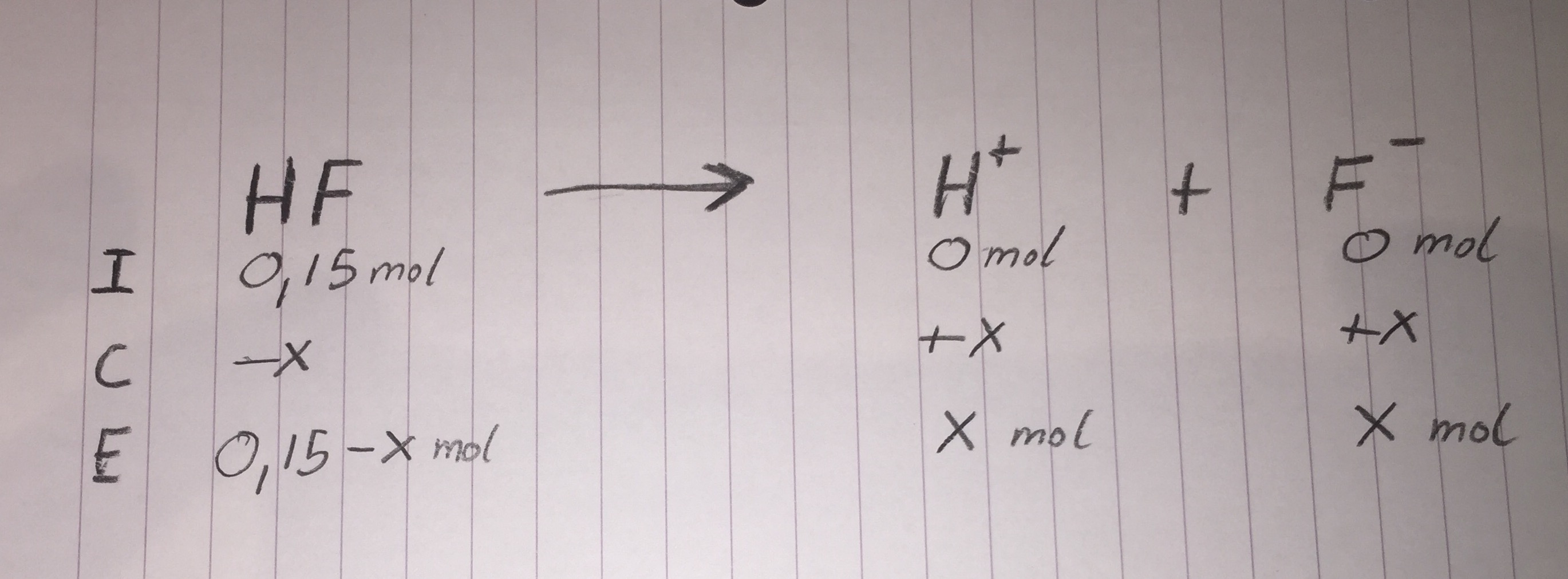
Finding X:
Because
We also know that
x=0.0101 (and a negative value, which we do not care about)
Therefore
Because
Now the conventional way of doing this
You know that what the Ka value is, is essentially:
Because
Hence, we end up with:
Now we have to make the assumption, that the concentration of the acid will initially bearly change, so we will keep it at 0.15M.
I.e.
Because
Now we can do the same for NaF
First we have to determine the Kb for NaF:
From here we can go through the same process as above:
Hence, the pOH is:
Hence
Lastly, we can find the pH of the mixture
I made an ICE table for you again:
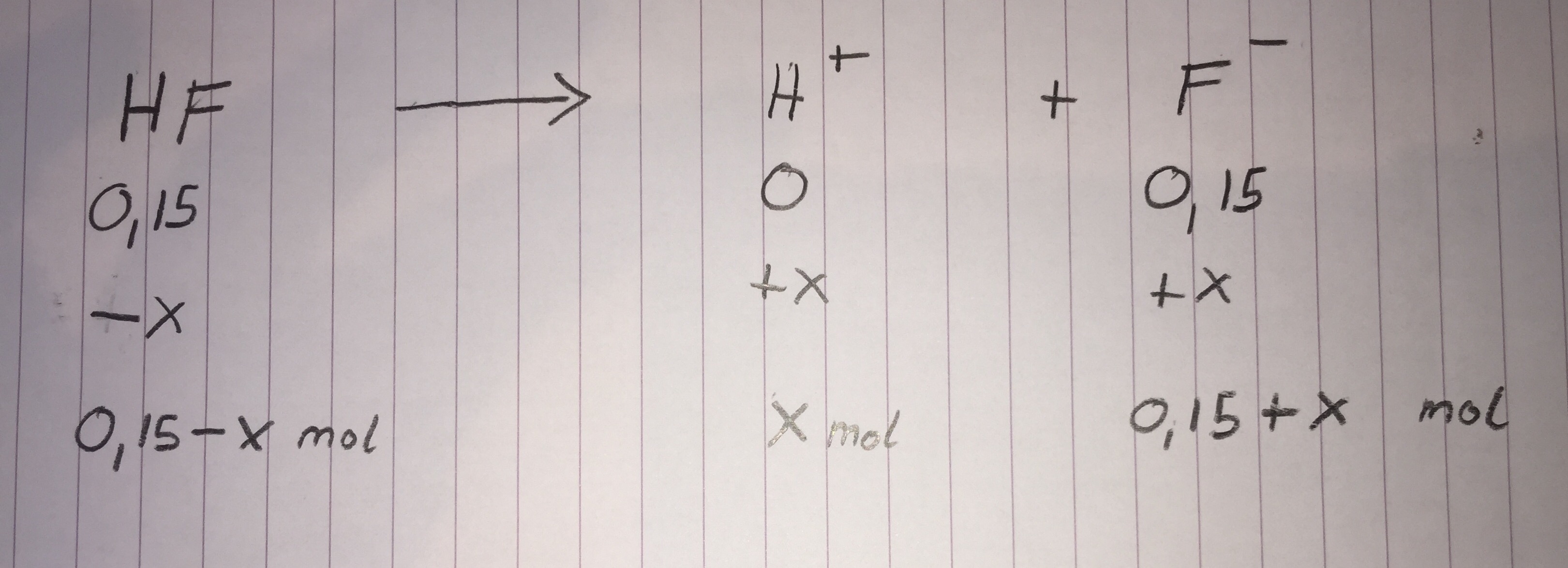
Note how the
Now solve in the same way that we did for the first part:
x=0.149 (and a negative value we do not care about)
Therefore
Hence, the pH is:

