Question

Question #75094

Answer 1

`csc(2arctan(3/4))=25/24`

Explanation:

Because `sin` and `csc` are reciprocals:

`csc(2arctan(3/4))=1/sin(2arctan(3/4))`

Using the double angle identity `sin(2theta)=2sin(theta)cos(theta)`:

`=1/(2color(blue)(sin(arctan(3/4)))color(red)(cos(arctan(3/4)))`

We can find the values of `sin(arctan(3/4))` and `cos(arctan(3/4))` using a similar method.

Note that when `theta=arctan(3/4)`, then `tan(theta)=3/4`. That is, where `theta` is an angle in a right triangle, the side opposite `theta` is `3` and the leg adjacent to `theta` is `4`. The Pythagorean theorem tells us that the hypotenuse is `5`.

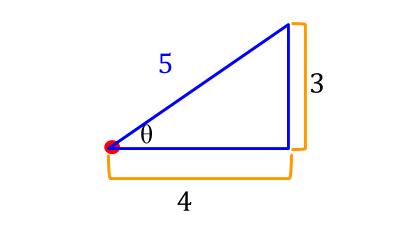
We then see that:

`color(blue)(sin(arctan(3/4)))=sin(theta)="opposite"/"hypotenuse"=3/5`

`color(red)(cos(arctan(3/4)))=cos(theta)="adjacent"/"hypotenuse"=4/5`

So the original expression is:

`=1/(2color(blue)((3/5))color(red)((4/5)))`

`=25/24`