Question

Question #d3c3a

Answer 1

`color(blue)(y<2x` and

`color(blue)(y > (6-2x)/3)`

Explanation:

We have two inequality expressions:

First expression is

`color(blue)(y<2x`

This inequality expression is already in simplified form.

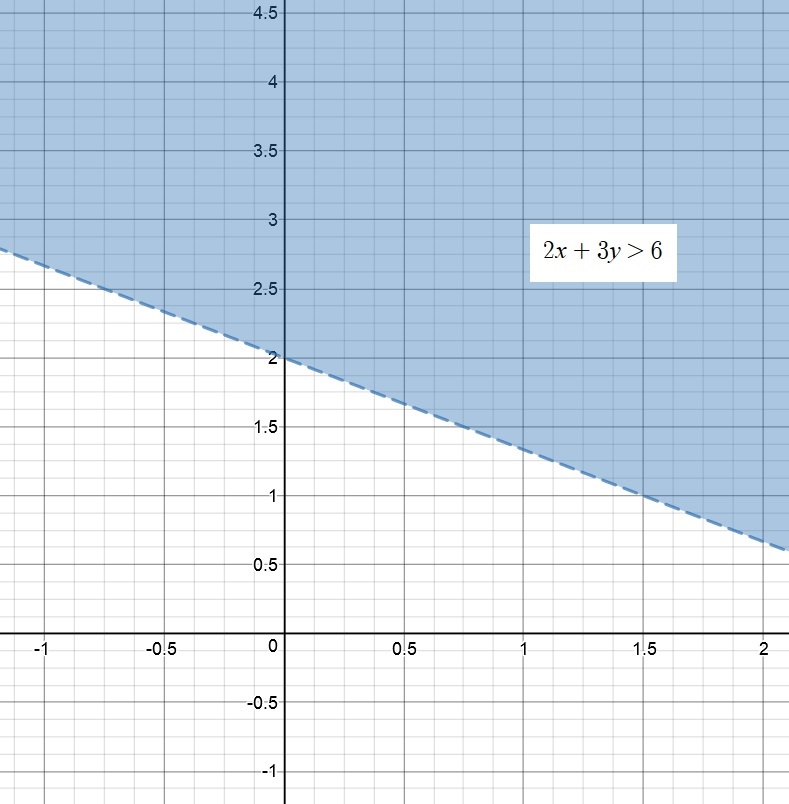
Next expression is

`color(blue)(2x+3y>6)`

We can simplify this expression by subtracting `color(red)(2x)` from both sides of the inequality.

`rArr 2x+3y-2x>6-2x`

In the next step we can cancel

`rArr cancel(2x)+3y cancel(-2x)>6-2x`

Hence, we get

`rArr 3y >6-2x`

Divide both sides of the inequality as shown below:

`rArr (3y)/3 >(6-2x)/3`

In the next step we can cancel

`rArr (cancel(3)y)/cancel 3 >(6-2x)/3`

Hence, our solution is

`rArr y >(6-2x)/3`

Hence we have two solutions

`color(blue)(y<2x` and

`color(blue)(y > (6-2x)/3)`

Please refer to the graphs below:

`color(blue)(y<2x`

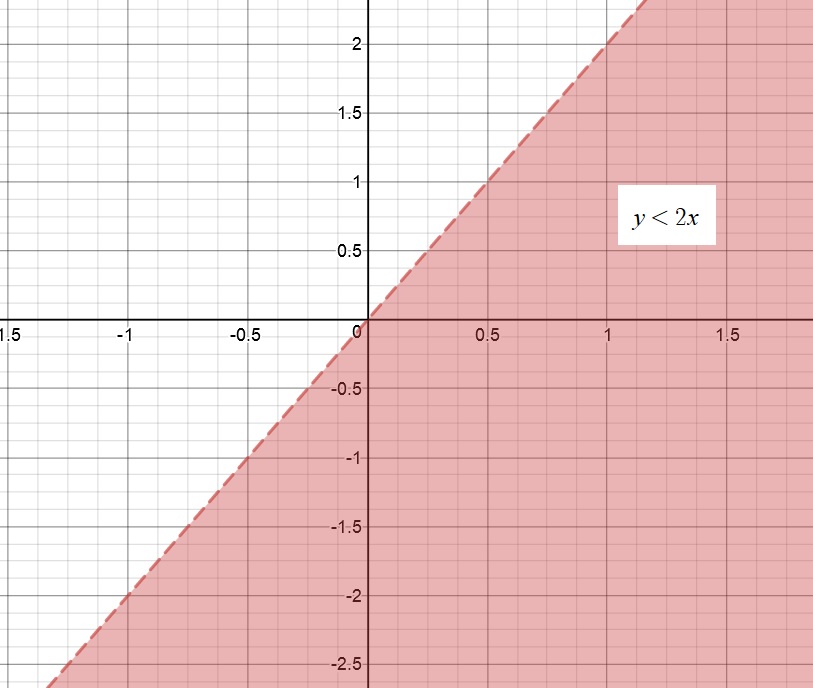
Next expression is

`color(blue)(2x+3y>6)`

Our simplified expression is

`color(blue)(y > (6-2x)/3)`

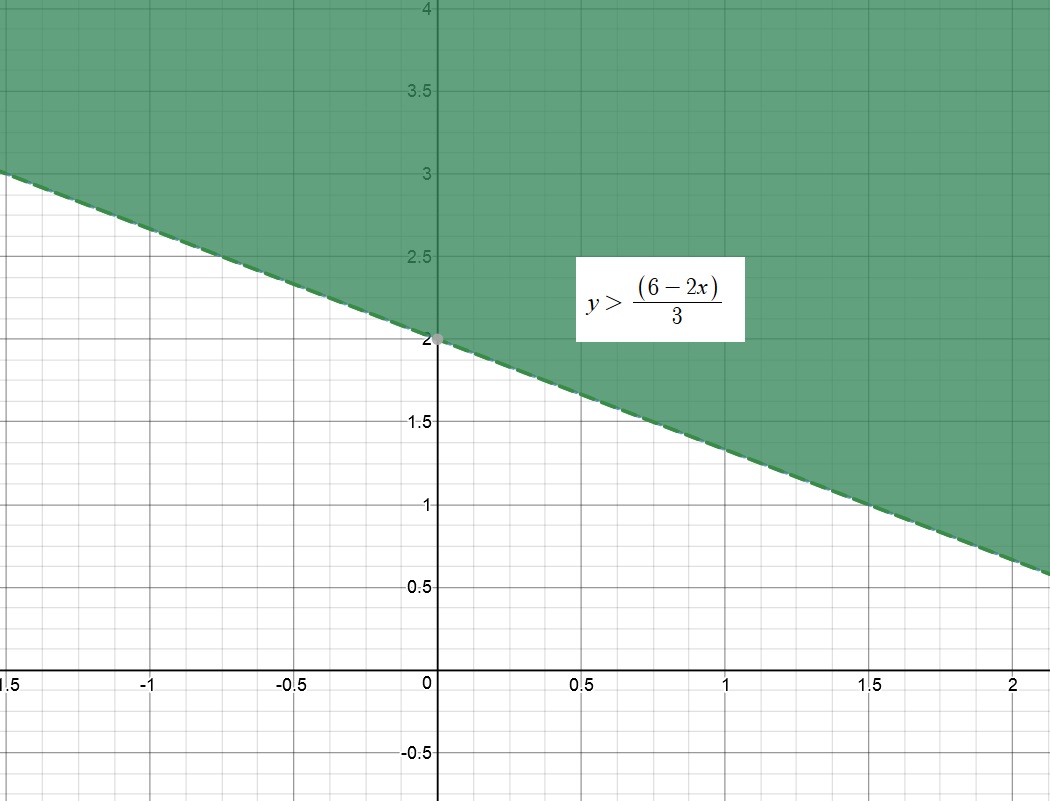
We observe that the last two graphs represent the same inequality.

Hope this helps.